题目内容
已知二次函数y=f(x)的图象是开口向上的抛物线,f(-5)、f(-1)、f(4)、f(7)这四个函数值中只有一个值不大于0.画草图分析这样的抛物线的位置特征,并写出满足已知条件的一个函数解析式,你还能写出其他的解析式吗?
考点:二次函数的性质
专题:数形结合
分析:由于f(-5)、f(-1)、f(4)、f(7)这四个函数值中只有一个值不大于0,可判断抛物线开口向下,于是可画出草图,于是可设a=-1,与x轴两交点的坐标为(-6,0),(6,0),则可利用交点式确定抛物线解析式,满足条件的解析式有很多,若只要改变a的值即可.
解答:解: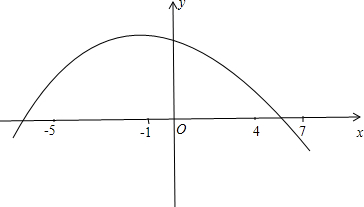 抛物线可为:抛物线开口向下,如图,
抛物线可为:抛物线开口向下,如图,
此时f(-5)、f(-1)、f(4)都大于0,f(7)小于0,
则抛物线与x轴的交点一个在点(-5,0)左侧,另一个交点在点(4,0)与(7,0)之间,
可设a=-1,与x轴两交点的坐标为(-6,0),(6,0),
所以y=-(x+6)(x-6)=-x2+36,
还可以写出其他的解析式,若令a=-2等.
 抛物线可为:抛物线开口向下,如图,
抛物线可为:抛物线开口向下,如图,此时f(-5)、f(-1)、f(4)都大于0,f(7)小于0,
则抛物线与x轴的交点一个在点(-5,0)左侧,另一个交点在点(4,0)与(7,0)之间,
可设a=-1,与x轴两交点的坐标为(-6,0),(6,0),
所以y=-(x+6)(x-6)=-x2+36,
还可以写出其他的解析式,若令a=-2等.
点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-
,
),对称轴直线x=-
,当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上;当a<0,抛物线开口向下.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |

练习册系列答案
相关题目
方程3x2+4x-2=0的根的情况是( )
| A、两个不相等的实数根 |
| B、两个相等的实数根 |
| C、没有实数根 |
| D、无法确定 |
把1400元的奖金按两种奖给22名学生,其中一等奖每人200元,二等奖每人50元,设获一等奖的学生有x人,则下列方程错误的是( )
| A、200x+50(22-x)=1400 | ||
B、
| ||
| C、20x+200(22-x)=1400 | ||
| D、(200-50)x+50×22=1400 |
下列说法中不正确的是( )
| A、在同一平面内,经过一点能画一条且只能画一条直线与已知直线垂直 |
| B、从直线外一点到这条直线的垂线段叫做点到直线的距离 |
| C、一条直线的垂线可以画无数条 |
| D、连接直线外一点与直线上各点的所有线段中,垂线段最短 |
