题目内容
 如图,已知⊙O是边长为2的等边△ABC的内切圆,则⊙O的面积为________.
如图,已知⊙O是边长为2的等边△ABC的内切圆,则⊙O的面积为________.

分析:欲求⊙O的面积,需先求出⊙O的半径;可连接OC,由切线长定理可得到∠OCB=∠OCA=30°,再连接OD(设BC切⊙O于D),在Rt△OCD中通过解直角三角形即可求得⊙O的半径,进而可求出⊙O的面积.
解答:
 解:设BC切⊙O于点D,连接OC、OD;
解:设BC切⊙O于点D,连接OC、OD;∵CA、CB都与⊙O相切,
∴∠OCD=∠OCA=30°;
Rt△OCD中,CD=
 BC=1,∠OCD=30°;
BC=1,∠OCD=30°;∴OD=CD•tan30°=
 ;
;∴S⊙O=π(OD)2=
 .
.点评:此题主要考查了三角形内切圆、切线长定理及解直角三角形等知识的综合应用.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
 列问题:
列问题: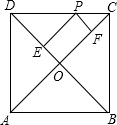 如图,已知P是边长为2的正方形ABCD的边CD任意一点,且PE⊥DB,垂足为E,PF⊥CA垂足为F,则PE+PF的长是
如图,已知P是边长为2的正方形ABCD的边CD任意一点,且PE⊥DB,垂足为E,PF⊥CA垂足为F,则PE+PF的长是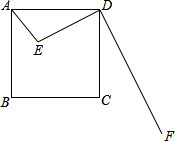 如图,已知E是边长为4cm的正方形ABCD内一点,且DE=3,∠AED=90°,DF⊥DE于D,在射线DF上是否存在这样的M,使得以C、D、M为顶点的三角形与△ADE相似?若存在,请求出满足条件的DM长;若不存在,请说明理由.
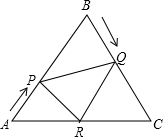
如图,已知E是边长为4cm的正方形ABCD内一点,且DE=3,∠AED=90°,DF⊥DE于D,在射线DF上是否存在这样的M,使得以C、D、M为顶点的三角形与△ADE相似?若存在,请求出满足条件的DM长;若不存在,请说明理由. 如图,已知P是边长为1的正三角形ABC内的一个动点,如PE⊥AB于E,PF⊥BC于F,PD⊥AC于D,则PD+PE+PF的值为( )
如图,已知P是边长为1的正三角形ABC内的一个动点,如PE⊥AB于E,PF⊥BC于F,PD⊥AC于D,则PD+PE+PF的值为( )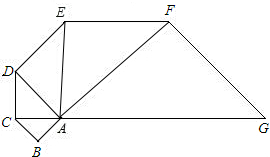 第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,如此类推.
第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,如此类推.