Question

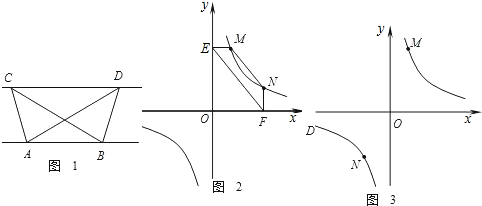
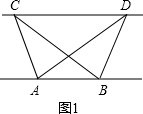
（1）探究新知：
如图1，已知△ABC与△ABD的面积相等，试判断AB与CD的位置关系，并说明理由．

（2）结论应用：
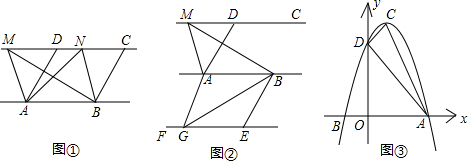
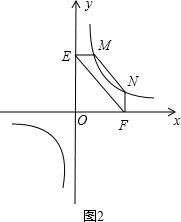
①如图2，点M，N在反比例函数y=

k

x

（k＞0）的图象上，过点M作ME⊥y轴，过点N作NF⊥x轴，垂足分别为E，F．
试证明：MN∥EF．

Answer 1

分析：（1）分别作两个三角形公共边上的高，由面积相等，则高相等，又同一直线上的两高平行，得四边形CDFE为矩形，则AB与CD的位置关系得定；
（2）连接MF、NE，先证明S_△MEF=S_△NEF，然后再运用（1）中的结论得证．

解答：解：（1）作CE⊥AB于E，DF⊥AB于F，则CE∥DF，
∵S_△ABC=S_△ABD，
∴

1

2

AB•CE=

1

2

AB•DF，CE=DF．
∴四边形CDFE为矩形，AB∥CD；


（2）连接MF、NE，过M作MP⊥EF，过N作NQ⊥EF，则MP∥NQ，
∴S_△MEF=

1

2

ME•OE=

1

2

k；S_△NEF=

1

2

NF•OF=

1

2

k，
∴S_△MEF=S_△NEF，且同底边EF，
∴M，N到EF的距离相等，即PM=NQ，
∴四边形MPQN为平行四边形，
∴MN∥EF．

点评：此题由浅入深探究问题，体现了数学化归思想．是一类比较创新的题型．同学们要擅于归纳总结．