题目内容
若△ABC是直角三角形,两条直角边分别为5和12,在三角形内有一点D,D到△ABC各边的距离都相等,则这个距离等于
- A.2
- B.3
- C.4
- D.5
A
分析:根据勾股定理列式求出斜边的长度,然后根据三角形的面积列式求解即可.
解答:∵Rt△ABC的两条直角边分别为5和12,
∴斜边=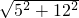 =13,
=13,
设D到△ABC各边的距离都相等为h,
则S△ABC= ×5×12=
×5×12= (5+12+13)•h,
(5+12+13)•h,
解得h=2.
故选A.
点评:本题考查了角平分线的性质,勾股定理的应用,本题利用三角形的面积列式求解更加简便.
分析:根据勾股定理列式求出斜边的长度,然后根据三角形的面积列式求解即可.
解答:∵Rt△ABC的两条直角边分别为5和12,
∴斜边=
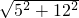 =13,
=13,设D到△ABC各边的距离都相等为h,
则S△ABC=
 ×5×12=
×5×12= (5+12+13)•h,
(5+12+13)•h,解得h=2.
故选A.
点评:本题考查了角平分线的性质,勾股定理的应用,本题利用三角形的面积列式求解更加简便.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
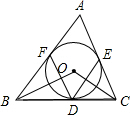 三角形的内切圆
三角形的内切圆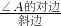 ,cosA=
,cosA=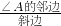 ,tanA=
,tanA= ,cotA=
,cotA=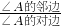
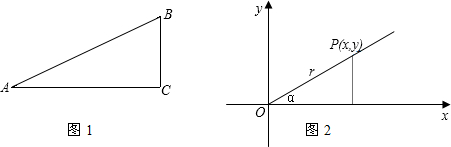
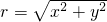 (r总是正的),然后把角α的三角函数规定为:
(r总是正的),然后把角α的三角函数规定为: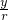 ,cosα=
,cosα=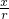 ,tanα=
,tanα= ,cotα=
,cotα=
 ),且cosα=
),且cosα=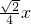 ,则tanα______;
,则tanα______;