Question

在三角形ABC中，AB=2，AC=，∠B=45°，则BC的长________．

Answer 1

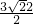
分析：首先根据正弦定理即可求得∠C的正弦值，然后分∠C是锐角和钝角两种情况进行讨论即可求解．
解答：解：∵在三角形ABC中，=，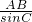
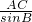∴sinC===，
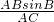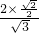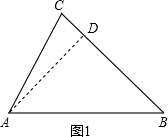
当∠C是锐角时如图1，作AD⊥AB于点D．
在直角△ACD中，sinC=，
∴AD=AC•sinC=，
则CD=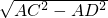=1，
在直角△ABD中，∠B=45°，则△ABD是等腰直角三角形，则BD=AB×=，
∴BC=CD+BD=；
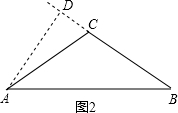当∠C是锐角时如图2，作AD⊥AB于点D，
同理，BD=，
在直角△ACD中，CD=1，
则BC=BD-CD=．
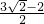故答案是：．
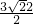点评：本题考查了正弦定理，以及三角函数，正确注意到分两种情况讨论是关键．