题目内容
13.直线y=-$\frac{n}{n+1}$x+$\frac{\sqrt{2}}{n+1}$(n为正整数)与坐标轴围成的三角形面积为Sn,则S1+S2+S3+…+S2015=$\frac{2015}{2016}$.分析 令x=0,y=0分别求出与y轴、x轴的交点,然后利用三角形面积公式列式表示出Sn,再利用拆项法整理求解即可.
解答 解:令x=0,则y=$\frac{\sqrt{2}}{n+1}$,
令y=0,则-$\frac{n}{n+1}$x+$\frac{\sqrt{2}}{n+1}$=0,
解得x=$\frac{\sqrt{2}}{n}$,
所以,Sn=$\frac{1}{2}×\frac{\sqrt{2}}{n+1}×\frac{\sqrt{2}}{n}$=$\frac{1}{n(n+1)}$•
所以,S1+S2+S3+…+S2015=$\frac{1}{2}+\frac{1}{2}×\frac{1}{3}+\frac{1}{3}×\frac{1}{4}+…+\frac{1}{2015}×\frac{1}{2016}$=$\frac{2015}{2016}$,
故答案为:$\frac{2015}{2016}$.
点评 本题考查的是一次函数图象上点的坐标特点,表示出Sn,再利用拆项法写成两个数的差是解题的关键,也是本题的难点.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
4.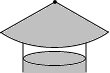 如图,要制作一个圆锥形的烟囱帽,使底面圆的半径与母线长的比是4:5,那么所需扇形铁皮的圆心角应为( )
如图,要制作一个圆锥形的烟囱帽,使底面圆的半径与母线长的比是4:5,那么所需扇形铁皮的圆心角应为( )
 如图,要制作一个圆锥形的烟囱帽,使底面圆的半径与母线长的比是4:5,那么所需扇形铁皮的圆心角应为( )
如图,要制作一个圆锥形的烟囱帽,使底面圆的半径与母线长的比是4:5,那么所需扇形铁皮的圆心角应为( )| A. | 288° | B. | 144° | C. | 216° | D. | 120° |
18.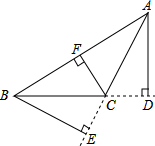 如图,∠ACB>90°,AD⊥BC,BE⊥AC,CF⊥AB,垂足分别为点D、点E、点F,△ABC中AC边上的高是( )
如图,∠ACB>90°,AD⊥BC,BE⊥AC,CF⊥AB,垂足分别为点D、点E、点F,△ABC中AC边上的高是( )
 如图,∠ACB>90°,AD⊥BC,BE⊥AC,CF⊥AB,垂足分别为点D、点E、点F,△ABC中AC边上的高是( )
如图,∠ACB>90°,AD⊥BC,BE⊥AC,CF⊥AB,垂足分别为点D、点E、点F,△ABC中AC边上的高是( )| A. | CF | B. | BE | C. | AD | D. | CD |
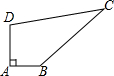 如图所示,一块四边形土地ABCD,∠A=90°,AB=6m,BC=24m,CD=26m,DA=8m,求四边形土地ABCD的面积.
如图所示,一块四边形土地ABCD,∠A=90°,AB=6m,BC=24m,CD=26m,DA=8m,求四边形土地ABCD的面积.