Question

【题目】直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2)

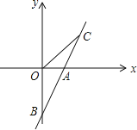
(1)求直线AB所对应的函数关系式;

(2)若直线AB上一点C在第一象限且点C的坐标为(a,2),求△BOC的面积.

Answer 1

【答案】(1)y=2x-2

(2)2

【解析】

（1）设直线AB的解析式为y=kx+b,将A(1,0),B(0,-2)分别代入解析式组成方程组，求k,b，从而得到解析式；（2）以OB为底，C到OB的垂线段长为高，根据三角形面积公式即可求解.

(1)解：设直线AB解析式为y=kx+b(k≠0)

将A(1,0),B(0,-2)代入，得

解得：

∴直线AB的解析式为y=2x-2

(2)解：∵C(a,2)在图象上，

∴2=2a-2

∴a=2, ∴C(2,2)

过点C作CH⊥x轴，垂足为H,如图

∴CH=2

∴△BOC的面积为·OB·CH=×2×2=2