Question

已知等腰梯形ABCD中，AD∥BC（AD＜BC），AB=CD=5，BC=12，沿着经过点A的直线翻折梯形ABCD，使点B落在直线AD上的点B′处，DB′=1，直线BB′与直线DC交于点H，则DH=________．

Answer 1

分析：分别根据当B点落在AD上或落在AD的延长线上利用相似三角形的判定与性质得出比例式即可求出．
解答：解：如图1所示：
∵AD∥BC，
∴△HB′D∽△HBC，
∴=，
∵AB=CD=5，BC=12，
∴=，
解得：HD=；
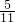如图2所示：
∵AD∥BC，
∴△HB′D∽△HBC，
∴=，
∵AB=CD=5，BC=12，
∴=，
解得：DH=．
故答案为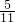：或．
点评：此题主要考查了相似三角形的判定与性质，利用相似三角形对应边之间的关系得出HD是解题关键．