题目内容
推理：如图，∵∠A=∠ACD，∠B=∠BCD，（已知）∴AD=CD，CD=DB（ 等腰三角形的性质）∴AD=DB，依据是
- A.旋转不改变图形的大小
- B.连接两点的所有线中线段最短
- C.等量代换
- D.整体大于部分
C
分析：由∠A=∠ACD，得AD=CD，再由∠B=∠BCD得CD=DB，利用等量代换即可解题．
解答：∵∠A=∠ACD，∴AD=CD，
∵∠B=∠BCD∴CD=DB，
因AD和DB都等于同一个量CD，
所以AD=DB，依据是等量代换．
故选C．
点评：此题考查学生对等腰三角形的判定与性质的理解和掌握，此题主要利用了等量代换求得两边相等．
分析：由∠A=∠ACD，得AD=CD，再由∠B=∠BCD得CD=DB，利用等量代换即可解题．
解答：∵∠A=∠ACD，∴AD=CD，
∵∠B=∠BCD∴CD=DB，
因AD和DB都等于同一个量CD，
所以AD=DB，依据是等量代换．
故选C．
点评：此题考查学生对等腰三角形的判定与性质的理解和掌握，此题主要利用了等量代换求得两边相等．
练习册系列答案
灵星计算小达人系列答案
孟建平错题本系列答案
相关题目
16、给出以下两个定理：
24、推理填空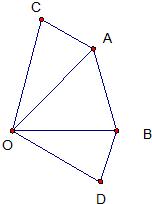
3、推理：如图，∵∠AOC=∠BOD，∴∠AOC+∠AOB=∠BOD+∠AOB，这个推理的依据是（ ）
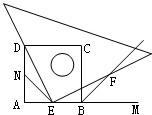13、（实验与推理）如图，四边形ABCD是正方形，M是AB延长线上一点．直角三角尺的一条直角边经过点D，且直角顶点E在AB边上滑动（点E不与点A，B重合），三角尺的另一条直角边与∠CBM的平分线BF相交于点F，当点E在AB边的中点位置时：
仔细想一想，完成下面的推理过程 如图，已知∠BED=∠B+∠D，试说明AB与CD的关系．