题目内容
 仔细想一想,完成下面的推理过程 如图,已知∠BED=∠B+∠D,试说明AB与CD的关系.
仔细想一想,完成下面的推理过程 如图,已知∠BED=∠B+∠D,试说明AB与CD的关系.解:AB∥CD,理由如下:
过点E作∠BEF=∠B
∴AB∥
EF
EF
(内错角相等,两直线平行
内错角相等,两直线平行
)∵∠BED=∠B+∠D(
已知
已知
)∴
∠DEF
∠DEF
=∠D (等量代换
等量代换
)∴
CD
CD
∥EF (内错角相等,两直线平行
内错角相等,两直线平行
)∴AB∥CD(
平行于同一条直线的两条直线平行
平行于同一条直线的两条直线平行
)分析:首先过点E作∠BEF=∠B,得出AB∥EF,再由∠BED=∠B+∠D,得出∠DEF=∠D,推出CD∥EF,从而得出AB∥CD.
解答:解:过点E作∠BEF=∠B,
∴AB∥EF(内错角相等,两直线平行),
∵∠BED=∠B+∠D(已知),
∴∠DEF=∠D(等量代换),
∴CD∥EF(内错角相等,两直线平行),
∴AB∥CD(平行于同一条直线的两条直线平行),
故答案分别为:EF,内错角相等,两直线平行,已知,∠DEF,等量代换,CD,内错角相等,两直线平行,平行于同一条直线的两条直线平行.
∴AB∥EF(内错角相等,两直线平行),
∵∠BED=∠B+∠D(已知),
∴∠DEF=∠D(等量代换),
∴CD∥EF(内错角相等,两直线平行),
∴AB∥CD(平行于同一条直线的两条直线平行),
故答案分别为:EF,内错角相等,两直线平行,已知,∠DEF,等量代换,CD,内错角相等,两直线平行,平行于同一条直线的两条直线平行.
点评:此题考查的知识点是平行线的判定与性质,关键是通过作角相等及等量代换说明AB与CD的关系.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 21、仔细想一想,完成下面的说理过程.
21、仔细想一想,完成下面的说理过程.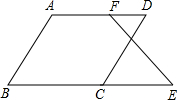 仔细想一想,完成下面的说理过程.
仔细想一想,完成下面的说理过程.
