Question

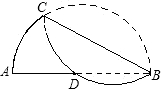
如图，AB是⊙O的一条弦，P是AB上的一点，PA=3，OP=PB=2，则⊙O的半径等于______．

Answer 1

∵PA=3，OP=PB=2，
∴AB=3+2=5，
过O作OD⊥AB于点D，连接OB，
则BD=

1

2

AB=

1

2

×5=

5

2

，
∵PB=2，
∴PD=

5

2

-2=

1

2

，
在Rt△ODP中，OD=

OP2-DP2

=

22-( 1 2 )2

=

15

2

，
在Rt△OBD中，OB=

OD2+BD2

=

( 15 2 )2+( 5 2 )2

=

10

．
故答案为：

10

．