题目内容
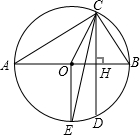
如图，AB是⊙O的直径，且AB=10，弦MN的长是6，若弦MN的两端在圆上滑动，始终与AB相交，设点A、B到MN的距离分别为h1，h2，则|h1-h2|等于______．
设AB、NM交于H，做OD⊥MN于D，连接OM，
∵AB是⊙O的直径，且AB=10，弦MN的长为6，
∴DN=DM=3，OD=4，
∵BE⊥MN，AF⊥MN，OD⊥MN，
∴BE∥OD∥AF，
∴△AFH∽△ODH∽△BEH，
∴
=
=
，
即
=
，
∴
=
=
，即
=
，
∴
（AF-BE）=-2，
∴|h1-h2|=|AF-BE|=8．
故答案为：8
∵AB是⊙O的直径，且AB=10，弦MN的长为6，
∴DN=DM=3，OD=4，
∵BE⊥MN，AF⊥MN，OD⊥MN，
∴BE∥OD∥AF，
∴△AFH∽△ODH∽△BEH，
∴
| AF |
| OD |
| AH |
| OH |
| 5-OH |
| OH |
即
| AF |
| 4 |
| 5-OH |
| OH |
∴
| BE |
| OD |
| HB |
| OH |
| 5+OH |
| OH |
| BE |
| 4 |
| 5+OH |
| OH |
∴
| 1 |
| 4 |
∴|h1-h2|=|AF-BE|=8．
故答案为：8
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
相关题目
