题目内容
分别指出，当x取何值时，下列各等式成立．
（1）
=2x；
（2）10x=0.01； （3）0.1x=100．
【答案】
（1）x=-5 （2）x=-2 （3）x=-2
【解析】
试题分析：根据负整数指数幂的运算法则，依次分析各小题即可得到结果。
（1）
，
；
（2）
，
；
（3）
，
；
考点：本题考查了负整数指数幂
点评：解答本题的关键是熟练掌握负整数指数幂的运算法则：
（a≠0，p是正整数）．
练习册系列答案
相关题目
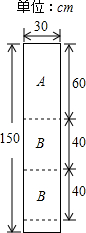某公司装修需用A型板材240块、B型板材180块，A型板材规格是60cm×30cm，B型板材规格是40cm×30cm．现只能购得规格是150cm×30cm的标准板材．一张标准板材尽可能多地裁出A型、B型板材，共有下列三种裁法：（如图是裁法一的裁剪示意图）
| 裁法一 | 裁法二 | 裁法三 | |
| A型板材块数 | 1 | 2 | 0 |
| B型板材块数 | 2 | m | n |
（1）上表中，m=
（2）分别求出y与x和z与x的函数关系式；
（3）若用Q表示所购标准板材的张数，求Q与x的函数关系式，并指出当x取何值时Q最小，此时按三种裁法各裁标准板材多少张？
（2009•河北）某公司装修需用A型板材240块、B型板材180块，A型板材规格是60cm×30cm，B型板材规格是40cm×30cm．现只能购得规格是150cm×30cm的标准板材．一张标准板材尽可能多地裁出A型、B型板材，共有下列三种裁法：（如图是裁法一的裁剪示意图）
设所购的标准板材全部裁完，其中按裁法一裁x张、按裁法二裁y张、按裁法三裁z张，且所裁出的A、B两种型号的板材刚好够用．
（1）上表中，m=______，n=______；
（2）分别求出y与x和z与x的函数关系式；
（3）若用Q表示所购标准板材的张数，求Q与x的函数关系式，并指出当x取何值时Q最小，此时按三种裁法各裁标准板材多少张？
| 裁法一 | 裁法二 | 裁法三 | |
| A型板材块数 | 1 | 2 | |
| B型板材块数 | 2 | m | n |
（1）上表中，m=______，n=______；
（2）分别求出y与x和z与x的函数关系式；
（3）若用Q表示所购标准板材的张数，求Q与x的函数关系式，并指出当x取何值时Q最小，此时按三种裁法各裁标准板材多少张？