Question

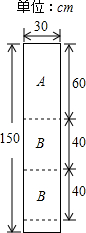（2013•本溪三模）某公司装修需要A型板材240块、B型板材180块，A型板材规格是60cm×30cm，B型板材规格是40cm×30cm．现只能购得规格是150cm×30cm的标准板材．一张标准板材尽可能多地裁出A型，B型板材，共有下列三种裁法，每种裁法所需费用如表所示：（如图是裁法一的裁剪示意图）

	裁法一	裁法二	裁法三
A型板材块数	1	2	0
B型板材块数	2	m	n
费用（元/张）	50	20	30

设所购的标准板材全部裁完，其中按裁法一裁x张，按裁法二裁y张，按裁法三裁z张，且所裁出的A，B两种型号的板材刚好够用，按裁法一裁出的张数不少于60张．
（1）上表中m=

0

，n=

3

；
（2）分别求出y与x和z与x的函数关系式；
（3）若w（元）表示三种裁法所需费用，求w与x的函数关系式，并指出当x取何值时w最小，此时按三种裁法各裁标准板材多少张．

Answer 1

分析：（1）结合图形和条件分析可以得出按裁法二裁剪时，所以无法裁出B型板，按裁法三裁剪时，3块B型板材块的长为120cm，120＜150，无法裁出4块B型板就可以得出结论；
（2）根据需要A型板材240块、B型板材180块及不同的裁法裁出的各种板材的数量建立方程就可以得出结论；
（3）由条件可以得出总费用W=三种裁法的费用之和，就可以求出W与x之间的函数关系式，再由条件求出建立关于x的不等式组求出x的取值范围就可以得出结论．

解答：解：（1）按裁法二裁剪时，2块A型板材块的长为120cm，150-120＜30，所以无法裁出B型板，
按裁法三裁剪时，3块B型板材块的长为120cm，120＜150，
而4块块B型板材块的长为160cm＞150，所以无法裁出4块B型板；
∴m=0，n=3．
故答案为：0，3；

（2）由题意，得
A型板块：240=x+2y，
∴y=120-0.5x；
B型板块：180=2x+3z，
z=60-

2

3

x．
∴y与x的函数关系式为y=120-0.5x，z与x的函数关系式为z=60-

2

3

x；

（3）由题意，得
W=50x+20y+30z，
=50x+20（120-0.5x ）+30（60-

2

3

x），
=20x+4200．
∵

120-0.5x≥0 60- 2 3 x≥0 x≥60

，
解得：60≤x≤90．
∵W=20x+4200，
∴k=20＞0，
∴W随x的增大而增大，
∴x=60时，W_最小=5400，
∴y=90张，z=20张．
答：此时按三种裁法各裁标准板数量为：裁法（1）60张，裁法（2）90张，裁法（3）20张．

点评：本题考查了一次函数的解析式的运用，一次函数的性质的运用，解不等式组的运用，解答时需要A型板材240块、B型板材180块及不同的裁法裁出的各种板材的数量建立方程求出解析式是求W关于x的解析式的关键．解答时理清题目的数量关系是重点．