题目内容
已知抛物线y=ax2+bx+c(a>0)的对称轴为直线x=1,且经过点(-1,y1)、(2,y2),则y1和y2的大小为( )
| A、y1>y2 |
| B、y1<y2 |
| C、y1=y2 |
| D、y1≥y2 |
考点:二次函数图象上点的坐标特征
专题:
分析:先根据抛物线的对称轴为x=11及A点的横坐标判断A点关于x=1对称点的坐标为(3,y1),再根据二次函数的二次函数的增减性进行解答.
解答:解:∵抛物线y=ax2+bx+c(a>0)的对称轴为直线x=1,
∴点(-1,y1)关于直线x=1的对称点坐标为(3,y1),
∵a>0,
∴图象的开口向上,x>1时,y随x的增大而增大,
∵3>2,
∴y1>y2.
故选A.
∴点(-1,y1)关于直线x=1的对称点坐标为(3,y1),
∵a>0,
∴图象的开口向上,x>1时,y随x的增大而增大,
∵3>2,
∴y1>y2.
故选A.
点评:本题考查的是二次函数图象上点的坐标特征,抛物线关于对称轴x=-
成轴对称,是本题的关键.
| b |
| 2a |

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
下列各组数为勾股数的是( )
| A、2、3、4 |
| B、8、15、16 |
| C、2.5、6、6.5 |
| D、5、12、13 |
下列计算正确的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、5-2
|
下列式子中,正确的是( )
| A、x2•x3=x6 |
| B、x6÷x2=x3 |
| C、x2+x3=x5 |
| D、(x2y)3=x6y3 |
下列计算正确的是( )
| A、x2•x3=x6 |
| B、(3xy)3=9x3y3 |
| C、(-2a2)2=-4a2 |
| D、(ab2)3=a3b6 |
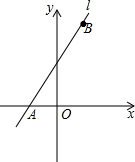 如图,已知直线l1经过点A(-1,0)和点B(1,4)
如图,已知直线l1经过点A(-1,0)和点B(1,4)