题目内容
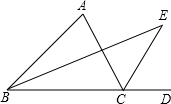 如图,∠ACD是△ABC的外角,BE平分∠ABC,CE平分∠ACD,且BE、CE交于E点.
如图,∠ACD是△ABC的外角,BE平分∠ABC,CE平分∠ACD,且BE、CE交于E点.
求证:∠E= ∠A.
∠A.
证明:∵∠ACD=∠A+∠ABC,
∴∠ECD= (∠A+∠ABC).
(∠A+∠ABC).
又∵∠ECD=∠E+∠EBC,
∴∠E+∠EBC= (∠A+∠ABC).
(∠A+∠ABC).
∵BE平分∠ABC,
∴∠EBC= ∠ABC,
∠ABC,
∴ ∠ABC+∠E=
∠ABC+∠E= (∠A+∠ABC),
(∠A+∠ABC),
∴∠E= ∠A.
∠A.
分析:由三角形的一个外角等于与它不相邻的两个内角的和,得∠ACD=∠A+∠ABC,∠ECD=∠E+∠EBC;由角平分线的性质,得∠ECD= (∠A+∠ABC),∠EBC=
(∠A+∠ABC),∠EBC= ∠ABC,利用等量代换,即可求得∠A与∠E的关系.
∠ABC,利用等量代换,即可求得∠A与∠E的关系.
点评:本题考查三角形外角的性质及三角形的角平分线性质,解答的关键是理清各角之间的关系.
∴∠ECD=
 (∠A+∠ABC).
(∠A+∠ABC).又∵∠ECD=∠E+∠EBC,
∴∠E+∠EBC=
 (∠A+∠ABC).
(∠A+∠ABC).∵BE平分∠ABC,
∴∠EBC=
 ∠ABC,
∠ABC,∴
 ∠ABC+∠E=
∠ABC+∠E= (∠A+∠ABC),
(∠A+∠ABC),∴∠E=
 ∠A.
∠A.分析:由三角形的一个外角等于与它不相邻的两个内角的和,得∠ACD=∠A+∠ABC,∠ECD=∠E+∠EBC;由角平分线的性质,得∠ECD=
 (∠A+∠ABC),∠EBC=
(∠A+∠ABC),∠EBC= ∠ABC,利用等量代换,即可求得∠A与∠E的关系.
∠ABC,利用等量代换,即可求得∠A与∠E的关系.点评:本题考查三角形外角的性质及三角形的角平分线性质,解答的关键是理清各角之间的关系.

练习册系列答案
相关题目
 14、如图,∠ACD是△ABC的外角,若∠ACD=125°,∠A=75°,则∠B=
14、如图,∠ACD是△ABC的外角,若∠ACD=125°,∠A=75°,则∠B= 21、如图,∠ACD是△ABC的一个外角,请你从下面三个条件中,选出两个作为已知条件,另一个作为结论,推出一个正确的命题.
21、如图,∠ACD是△ABC的一个外角,请你从下面三个条件中,选出两个作为已知条件,另一个作为结论,推出一个正确的命题. 如图,∠ACD是△ABC的外角,BE平分∠ABC,CE平分∠ACD,且BE、CE交于E点.
如图,∠ACD是△ABC的外角,BE平分∠ABC,CE平分∠ACD,且BE、CE交于E点. 如图,∠ACD是△ABC的外角,若∠ACD=135°,∠A=75°,则∠B=
如图,∠ACD是△ABC的外角,若∠ACD=135°,∠A=75°,则∠B= 如图,∠ACD是△ABC的外角,∠A=50°,∠ACD=110°,
如图,∠ACD是△ABC的外角,∠A=50°,∠ACD=110°,