题目内容
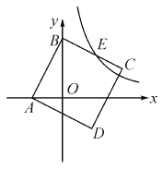
【题目】如图，正方形
的顶点
分别在
轴和
轴上，与双曲线
恰好交于
的中点
. 若
，则
的值为（ ）
A.6B.8C.10D.12
【答案】D
【解析】
作EH⊥x轴于点H，EG⊥y轴于点G，根据“OB=2OA”分别设出OB和OA的长度，利用矩形的性质得出△EBG∽△BAO，再根据相似比得出BG和EG的长度，进而写出点E的坐标代入反比例函数的解析式，即可得出答案.
作EH⊥x轴于点H，EG⊥y轴于点G
设AO=a，则OB=2OA=2a
∵ABCD为正方形
∴∠ABC=90°，AB=BC
∵EG⊥y轴于点G
∴∠EGB=90°
∴∠EGB=∠BOA=90°
∠EBG+∠BEG=90°
∴∠BEG=∠ABO
∴△EBG∽△BAO
∴
∵E是BC的中点
∴
∴
∴BG=
，EG=a
∴OG=BO-BG=
∴点E的坐标为
∵E在反比例函数上面
∴
解得：
∴AO=
，BO=
故答案选择D.
练习册系列答案
相关题目
