Question

【题目】已知二次函数y＝ax＋bx－4(a，b是常数.且a0)的图象过点(3，－1).

(1)试判断点(2，2－2a)是否也在该函数的图象上，并说明理由.

(2)若该二次函数的图象与x轴只有一个交点，求该函数表达式.

(3)已知二次函数的图像过(，)和(，)两点，且当＜时，始终都有＞，求a的取值范围.

Answer 1

【答案】（1）不在；（2）；；（3）

【解析】

（1）将点代入函数解析式，求出a和b的等式，将函数解析式改写成只含有a的形式，再将点代入验证即可；

（2）令，得到一个一元二次方程，由题意此方程只有一个实数根，由根的判别式即可求出a的值，从而可得函数表达式；

（3）根据函数解析式求出其对称轴，再根据函数图象的增减性判断即可.

（1）二次函数图像过点

代入得，

，代入得

将代入得，得，不成立，所以点不在该函数图像上；

（2）由（1）知，

与x轴只有一个交点

只有一个实数根

，或

当时，，所以表达式为：

当时，，所以表达式为：；

（3）

对称轴为

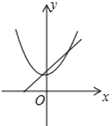
当时，函数图象如下：

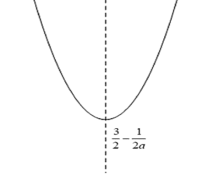
若要满足时，恒大于，则、均在对称轴左侧

，

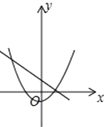
当时，函数图象如下：

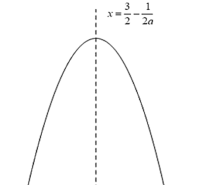
，此时，必小于

综上，所求的a的取值范围是：.