题目内容
(2014•宁波一模)(1)先化简,再求值:
÷
-
,其中a=
-2.
(2)解不等式组:
.
| a2+3a |
| a2+4a+4 |
| a+3 |
| a+2 |
| 2 |
| a+2 |
| 2 |
(2)解不等式组:
|
分析:(1)先根据分式混合运算的法则把原式进行化简,再把a的值代入进行计算即可;
(2)分别求出各不等式的解集,再求出其公共解集即可.
(2)分别求出各不等式的解集,再求出其公共解集即可.
解答:解:(1)原式=
•
-
=
-
=
,
当a=
-2时,原式=
=1-2
;
(2)
,
由①得,x>-1,
由②得,x<
,
故此不等式组的解集为:-1<x<
.
| a(a+3) |
| (a+2)2 |
| a+2 |
| a+3 |
| 2 |
| a+2 |
=
| a |
| a+2 |
| 2 |
| a+2 |
=
| a-2 |
| a+2 |
当a=
| 2 |
| ||
|
| 2 |
(2)
|
由①得,x>-1,
由②得,x<
| 1 |
| 5 |
故此不等式组的解集为:-1<x<
| 1 |
| 5 |
点评:本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目

 (2014•宁波一模)如图,在正方形ABCD中,对角线AC,BD交于点O,折叠正方形ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展平后,折痕DE分别交AB,AC于点E,G,连接GF,下列结论:①AE=AG;②tan∠AGE=2;③S△DOG=S四边形EFOG;④四边形ABFG为等腰梯形;⑤BE=2OG,则其中正确的结论个数为( )
(2014•宁波一模)如图,在正方形ABCD中,对角线AC,BD交于点O,折叠正方形ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展平后,折痕DE分别交AB,AC于点E,G,连接GF,下列结论:①AE=AG;②tan∠AGE=2;③S△DOG=S四边形EFOG;④四边形ABFG为等腰梯形;⑤BE=2OG,则其中正确的结论个数为( )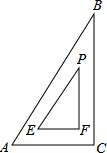 (2014•宁波一模)如图是一把30°的三角尺,外边AC=8,内边与外边的距离都是2,那么EF的长度是( )
(2014•宁波一模)如图是一把30°的三角尺,外边AC=8,内边与外边的距离都是2,那么EF的长度是( )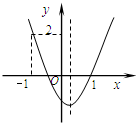 (2014•宁波一模)如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(-1,2)和(1,0),且与y轴相交于负半轴.给出四个结论:①abc<0;②a+c=1;③2a+b<0;④b2-4ac>0.其中结论正确的个数为( )
(2014•宁波一模)如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(-1,2)和(1,0),且与y轴相交于负半轴.给出四个结论:①abc<0;②a+c=1;③2a+b<0;④b2-4ac>0.其中结论正确的个数为( )