题目内容
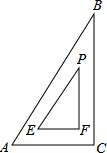 (2014•宁波一模)如图是一把30°的三角尺,外边AC=8,内边与外边的距离都是2,那么EF的长度是( )
(2014•宁波一模)如图是一把30°的三角尺,外边AC=8,内边与外边的距离都是2,那么EF的长度是( )分析:解直角三角形求出AC,延长EF交BC于N,延长FE交AB于M,过E作EG⊥AB于G,证△BMN∽△BAC,求出MN,解直角三角形求出ME,即可求出答案.
解答: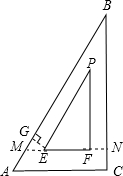
解:在Rt△BAC中,∠C=90°,AC=8,∠A=60°,
∴BC=AC×tan60°=8
,
延长EF交BC于N,延长FE交AB于M,过E作EG⊥AB于G,
∵EF∥AC,
∴∠BMN=∠A=60°,△BMN∽△BAC,
∴
=
,
∴
=
,
解得:MN=8-
,
∵GE⊥AB,
∴∠EGM=90°,
∵∠GME=60°,GE=2,
∴ME=
=
,
∴EF=MN-ME-FN
=8-
-2-
=6-2
,
故选D.

解:在Rt△BAC中,∠C=90°,AC=8,∠A=60°,
∴BC=AC×tan60°=8
| 3 |
延长EF交BC于N,延长FE交AB于M,过E作EG⊥AB于G,
∵EF∥AC,
∴∠BMN=∠A=60°,△BMN∽△BAC,
∴
| MN |
| AC |
| BN |
| BC |
∴
| MN |
| 8 |
8
| ||
8
|
解得:MN=8-
| 2 |
| 3 |
| 3 |
∵GE⊥AB,
∴∠EGM=90°,
∵∠GME=60°,GE=2,
∴ME=
| GE |
| cos60° |
| 4 |
| 3 |
| 3 |
∴EF=MN-ME-FN
=8-
| 2 |
| 3 |
| 3 |
| 4 |
| 3 |
| 3 |
| 3 |
故选D.
点评:本题考查了解直角三角形和相似三角形的性质和判定的应用,关键是求出NF、MN、EM的值.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目

 (2014•宁波一模)如图,在正方形ABCD中,对角线AC,BD交于点O,折叠正方形ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展平后,折痕DE分别交AB,AC于点E,G,连接GF,下列结论:①AE=AG;②tan∠AGE=2;③S△DOG=S四边形EFOG;④四边形ABFG为等腰梯形;⑤BE=2OG,则其中正确的结论个数为( )
(2014•宁波一模)如图,在正方形ABCD中,对角线AC,BD交于点O,折叠正方形ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展平后,折痕DE分别交AB,AC于点E,G,连接GF,下列结论:①AE=AG;②tan∠AGE=2;③S△DOG=S四边形EFOG;④四边形ABFG为等腰梯形;⑤BE=2OG,则其中正确的结论个数为( )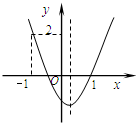 (2014•宁波一模)如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(-1,2)和(1,0),且与y轴相交于负半轴.给出四个结论:①abc<0;②a+c=1;③2a+b<0;④b2-4ac>0.其中结论正确的个数为( )
(2014•宁波一模)如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(-1,2)和(1,0),且与y轴相交于负半轴.给出四个结论:①abc<0;②a+c=1;③2a+b<0;④b2-4ac>0.其中结论正确的个数为( )