题目内容
 如图,在△ABC中,AB=AC,BC=5cm,作AB的垂直平分线交另一于D,连接BD,如果△BCD的周长是17cm,则AB=
如图,在△ABC中,AB=AC,BC=5cm,作AB的垂直平分线交另一于D,连接BD,如果△BCD的周长是17cm,则AB=考点:线段垂直平分线的性质,等腰三角形的性质
专题:
分析:先根据线段垂直平分线的性质得出AD=BD,再根据△BCD的周长是17cm求出BD+CD的长,进而得出结论.
解答:解:∵DE是线段AB的垂直平分线,
∴AD=BD,
∵△BCD的周长是17cm,
∴BD+CD=17-BC=17-5=12cm,
∴BD+CD=AD+CD=AC,
∴AC=12cm,
∵AB=AC,
∴AB=12cm.
故答案为:12.
∴AD=BD,
∵△BCD的周长是17cm,
∴BD+CD=17-BC=17-5=12cm,
∴BD+CD=AD+CD=AC,
∴AC=12cm,
∵AB=AC,
∴AB=12cm.
故答案为:12.
点评:本题考查的是线段垂直平分线的性质,熟知垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.

练习册系列答案
相关题目
甲、乙、丙三种商品,若购买甲3件、乙2件、丙1件,共需315元钱,购甲1件、乙2件、丙3件共需285元钱,那么购甲、乙、丙三种商品各一件共需多少钱( )
| A、128元 |
| B、130元 |
| C、150 元 |
| D、160元 |
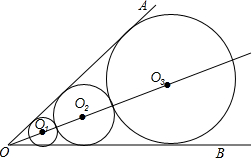 如图,∠AOB=60°,O1,O2,O3…是∠AOB平分线上的点,其中OO1=2,若分别以O1,O2,O3…为圆心作圆,使得⊙O1,⊙O2,⊙O3…均与∠AOB的两边相切,且相邻两圆相外切,则⊙O2014的面积是
如图,∠AOB=60°,O1,O2,O3…是∠AOB平分线上的点,其中OO1=2,若分别以O1,O2,O3…为圆心作圆,使得⊙O1,⊙O2,⊙O3…均与∠AOB的两边相切,且相邻两圆相外切,则⊙O2014的面积是