Question

【题目】如图，菱形中，，点是上一点，，，，，则的长是________．

Answer 1

【答案】

【解析】

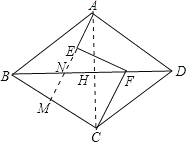
连接AC交BD于H，延长AE与BC交于点M，交BH于点N，根据菱形的性质可以得到△ABC是等边三角形，∠BCA＝60°，构造△ANH≌△CHF，利用勾股定理求得线段AN、NF、CH的长度可以求得AM的长度，即可得到答案．

如图所示，连接AC交BD于H，延长AE与BC交于点M，交BH于点N，

在△ANH和△CHF中，

，

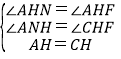∴△ANH≌△CHF（AAS），

∴NH＝HF，AN＝CF，

∵四边形ABCD是菱形，∠BCD＝120°，

∴∠BCA＝60°，且BA＝BC，

∴△ABC是等边三角形，

∴AB＝AC

又∵EF⊥CF，AE⊥EF，AE＝3，EF＝4，根据勾股定理：

∴AF＝CF＝AN＝5，EN＝2，

又∵EF＝4，

∴NF＝＝2，

∴NH＝HF＝，

∴CH＝＝2，

∴AB＝BC＝＝2×2＝4．

故答案为：4．