题目内容
7.已知直线y=kx+b经过点(1,5)和(-1,1).(1)求这个一次函数的解析式;
(2)求关于x的不等式kx+b≥5的解集.
分析 (1)将两点代入,运用待定系数法求解;
(2)把y=5代入y=2x+3解得,x=1,然后根据一次函数是增函数,进而得到关于x的不等式kx+b≥5的解集是x≥1.
解答 解:(1)∵一次函数y=kx+b的图象经过点(1,5)和(-1,1),
∴$\left\{\begin{array}{l}{k+b=5}\\{-k+b=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=2}\\{b=3}\end{array}\right.$
∴函数解析式为:y=2x+3;
(2)∵k=2>0,
∴y随x的增大而增大,
把y=5代入y=2x+3解得,x=1,
∴当x≥1时,函数y≥5,
故不等式kx+b≥5的解集为x≥1.
点评 本题考查待定系数法求函数解析式,一次函数与一元一次不等式,关键是掌握数形结合思想.认真体会一次函数与一元一次不等式之间的内在联系.

练习册系列答案
相关题目
15.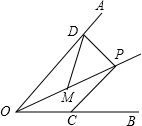 如图,已知点P是∠AOB角平分线上的一点,∠AOB=60°,PD⊥OA,M是OP的中点,DM=4cm,如果点C是OB上一个动点,则PC的最小值为( )
如图,已知点P是∠AOB角平分线上的一点,∠AOB=60°,PD⊥OA,M是OP的中点,DM=4cm,如果点C是OB上一个动点,则PC的最小值为( )
 如图,已知点P是∠AOB角平分线上的一点,∠AOB=60°,PD⊥OA,M是OP的中点,DM=4cm,如果点C是OB上一个动点,则PC的最小值为( )
如图,已知点P是∠AOB角平分线上的一点,∠AOB=60°,PD⊥OA,M是OP的中点,DM=4cm,如果点C是OB上一个动点,则PC的最小值为( )| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{3}$ |
2.在实数-4、0、2、5中,最小的实数是( )
| A. | -4 | B. | 0 | C. | 2 | D. | 5 |
16.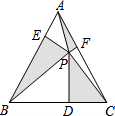 如图,等边△ABC中,P为三角形内一点,过P作PD⊥BC,PE⊥AB,PF⊥AC,连结AP、BP、CP,如果S△APF+S△BPE+S△PCD=$\frac{9\sqrt{3}}{2}$,那么△ABC的内切圆半径为( )
如图,等边△ABC中,P为三角形内一点,过P作PD⊥BC,PE⊥AB,PF⊥AC,连结AP、BP、CP,如果S△APF+S△BPE+S△PCD=$\frac{9\sqrt{3}}{2}$,那么△ABC的内切圆半径为( )
 如图,等边△ABC中,P为三角形内一点,过P作PD⊥BC,PE⊥AB,PF⊥AC,连结AP、BP、CP,如果S△APF+S△BPE+S△PCD=$\frac{9\sqrt{3}}{2}$,那么△ABC的内切圆半径为( )
如图,等边△ABC中,P为三角形内一点,过P作PD⊥BC,PE⊥AB,PF⊥AC,连结AP、BP、CP,如果S△APF+S△BPE+S△PCD=$\frac{9\sqrt{3}}{2}$,那么△ABC的内切圆半径为( )| A. | 1 | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{3}$ | D. | 2 |
17.某校举行“汉字听写”比赛,每位学生听写汉字39个,比赛后随机抽查部分学生听写结果,以下是根据抽查结果绘制的统计图的一部分.根据信息解决下列问题:
(1)本次共随机抽查了100名学生,并补全条形统计图;
(2)若把每组听写正确的个数用这组数据的组中值代替,则被抽查学生听写正确的个数的平均数是多少?
(3)该校共有1500名学生,如果听写正确的个数少于24个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.

| 组别 | 听写正确的个数x | 组中值 |
| A | 0≤x<8 | 4 |
| B | 8≤x<16 | 12 |
| C | 16≤x<24 | 20 |
| D | 24≤x<32 | 28 |
| E | 32≤x<40 | 36 |
(2)若把每组听写正确的个数用这组数据的组中值代替,则被抽查学生听写正确的个数的平均数是多少?
(3)该校共有1500名学生,如果听写正确的个数少于24个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.

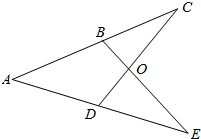 如图,已知B、D分别是AC、AE的中点,且AB=AD,OD=OB,求证:OE=OC.
如图,已知B、D分别是AC、AE的中点,且AB=AD,OD=OB,求证:OE=OC.