题目内容
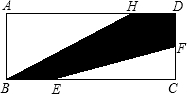 已知:如图,长方形ABCD中,F是CD的中点,BC=3BE,AD=4HD.若长方形的面积是300平方米,则阴影部分的面积等于
已知:如图,长方形ABCD中,F是CD的中点,BC=3BE,AD=4HD.若长方形的面积是300平方米,则阴影部分的面积等于137.5
137.5
平方米.分析:阴影部分的面积可由矩形的面积与△EFC、△ABH的差表示,又由题中条件可得出两个三角形面积与矩形面积的关系,进而代入数据求解即可.
解答:解:∵矩形的面积是300,即SABCD=BC•AB=300,
又BC=3BE,AD=4HD,
∴S△EFC=
EC•FC=
•
BC•
CD=
BC•AB,
S△ABH=
•AB•AH=
•AB•
AD=
BC•AB,
则S阴影=SABCD-S△EFC-S△ABH=BC•AB-
BC•AB-
BC•AB=
BC•AB=
×300=137.5平方米.
故此题答案为137.5.
又BC=3BE,AD=4HD,
∴S△EFC=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
S△ABH=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 8 |
则S阴影=SABCD-S△EFC-S△ABH=BC•AB-
| 1 |
| 6 |
| 3 |
| 8 |
| 11 |
| 24 |
| 11 |
| 24 |
故此题答案为137.5.
点评:本题主要考查了矩形的性质及矩形、三角形面积的计算,应熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (15届江苏初二1试)已知:如图,长方形ABCD被两条线段分割成四个小长方形,如果其中图形Ⅰ、Ⅱ、Ⅲ的面积依次为8、6、5,则阴影部分的面积为
(15届江苏初二1试)已知:如图,长方形ABCD被两条线段分割成四个小长方形,如果其中图形Ⅰ、Ⅱ、Ⅲ的面积依次为8、6、5,则阴影部分的面积为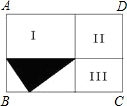 已知:如图,长方形ABCD被两条线段分割成四个小长方形,如果其中图形Ⅰ、Ⅱ、Ⅲ的面积依次为4、3、2,则阴影部分的面积为
已知:如图,长方形ABCD被两条线段分割成四个小长方形,如果其中图形Ⅰ、Ⅱ、Ⅲ的面积依次为4、3、2,则阴影部分的面积为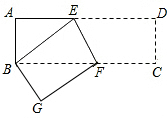 已知,如图,长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则AE=
已知,如图,长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则AE=