题目内容
7.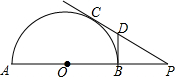 如图,PC是半圆的切线,且PB=OB,过B的切线交PC于D,若PC=6,则⊙O半径为$\sqrt{3}$,CD:DP=$\frac{1}{2}$.
如图,PC是半圆的切线,且PB=OB,过B的切线交PC于D,若PC=6,则⊙O半径为$\sqrt{3}$,CD:DP=$\frac{1}{2}$.
分析 连接OC,由PC是半圆的切线,得到∠OCP=90°,根据直角三角形的性质得到∠P=30°,解直角三角形得到结论.
解答  解:连接OC,
解:连接OC,
∵PC是半圆的切线,
∴∠OCP=90°,
∵OC=OB,PB=OB,
∴OC=$\frac{1}{2}$OP,
∴∠P=30°,
∴tan∠P=$\frac{OC}{PC}$=$\frac{\sqrt{3}}{3}$,
∵PC=6,
∴OC=2$\sqrt{3}$,
∴⊙O半径为2$\sqrt{3}$,
∵DB⊙O的切线,
∴∠DBP=∠DBO=90°,
∴cos∠P=$\frac{PB}{PD}$=$\frac{\sqrt{3}}{2}$,
∵PB=OB=2$\sqrt{3}$,
∴PD=4,
∴CD=2,
∴CD:DP=$\frac{1}{2}$,
故答案为:$\sqrt{3}$,$\frac{1}{2}$.
点评 本题考查了切线的性质,解直角三角形,正确的作出辅助线是解题的关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
16.Rt△ABC中,AB=3,∠BAC=90°,M是斜边BC上一点,将三角ABM沿AM翻折后,B恰好落在AC的三等分点,则M到直线AC的距离是$\frac{9}{4}$或$\frac{9}{5}$.
17.若(x2-x)(x2-x-2)-8=0,则x2-x的值是( )
| A. | -2 | B. | 4 | C. | -2或4 | D. | -4或2 |
 如图,在矩形ABCD中,AB=2cm,BC=4cm,点P从点A出发,沿AB以1cm/s的速度向点B匀速运动,同时点Q从点D出发,沿D-C-B以3cm/s的速度向点B匀速运动,连接PQ、BQ,设点P的运动时间为t(s),△BPQ的面积为S(cm2)
如图,在矩形ABCD中,AB=2cm,BC=4cm,点P从点A出发,沿AB以1cm/s的速度向点B匀速运动,同时点Q从点D出发,沿D-C-B以3cm/s的速度向点B匀速运动,连接PQ、BQ,设点P的运动时间为t(s),△BPQ的面积为S(cm2) 如图,AB=AC=AD,这可以说明,点B,C和D都在以点A为圆心,以AB为半径的圆上.
如图,AB=AC=AD,这可以说明,点B,C和D都在以点A为圆心,以AB为半径的圆上.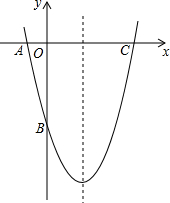 如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A(-1,0)和点B(0,-5).
如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A(-1,0)和点B(0,-5).