题目内容
 如图,将两个边长为2cm且互相重合的正方形纸片沿对角线翻折成等腰直角三角形后,再抽出一个等腰直角三角形沿AC边移动,若重叠部分面积为1cm2,则它移动的距离AA′为
如图,将两个边长为2cm且互相重合的正方形纸片沿对角线翻折成等腰直角三角形后,再抽出一个等腰直角三角形沿AC边移动,若重叠部分面积为1cm2,则它移动的距离AA′为2
-2
| 2 |
2
-2
cm.| 2 |
分析:根据题意可求得阴影部分是一个等腰直角三角形,且可求得其直角边与斜边的长,同时可得到原来等腰直角三角形的斜边的长,则再求它移动的距离就不难了.
解答:解:根据题意得:AB∥A′B′,BC∥B′C′,
∴∠A′PC=∠B=90°,
∵∠A=∠CA′P=∠ACP=45°,
∴△A′PC是等腰直角三角形,
∵△A′PC的面积是1cm2,
∴S△A′PC=
A′P•PC=1(cm2),
∴A′P=PC=
cm,
∴A′C=2cm,
由于原等腰直角三角形的斜边是2
cm,
所以平移的距离是:2
-2(cm).
故答案为2
-2.
∴∠A′PC=∠B=90°,
∵∠A=∠CA′P=∠ACP=45°,
∴△A′PC是等腰直角三角形,
∵△A′PC的面积是1cm2,
∴S△A′PC=
| 1 |
| 2 |
∴A′P=PC=
| 2 |
∴A′C=2cm,
由于原等腰直角三角形的斜边是2
| 2 |
所以平移的距离是:2
| 2 |
故答案为2
| 2 |
点评:此题主要考查学生对正方形的性质及等腰三角形的性质的理解及运用.

练习册系列答案
相关题目
 如图,将两个边长为
如图,将两个边长为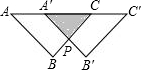 如图,将两个边长为2cm且互相重合的正方形纸片沿对角线翻折成等腰直角三角形后,再抽出一个等腰直角三角形沿AC边移动,若重叠部分面积为1cm2,则它移动的距离AA′为________cm.
如图,将两个边长为2cm且互相重合的正方形纸片沿对角线翻折成等腰直角三角形后,再抽出一个等腰直角三角形沿AC边移动,若重叠部分面积为1cm2,则它移动的距离AA′为________cm. 如图,将两个边长为
如图,将两个边长为 的正方形沿对角线剪开,将所得的四个三角形拼成一个大正方形,则这个大正方形的边长是________.
的正方形沿对角线剪开,将所得的四个三角形拼成一个大正方形,则这个大正方形的边长是________.