题目内容
 如图,点M,N分别在等边三角形ABC的BC、CA边上,且BM=CN,AM,BN交于点Q.
如图,点M,N分别在等边三角形ABC的BC、CA边上,且BM=CN,AM,BN交于点Q.(1)求证:∠BQM=60°.
(2)思考下列问题:
①如果将原题中“BM=CN”与“∠BQM=60°”的位置交换,得到的新命题是否仍是真命题?
②如果将原题中的点M,N分别移动到BC,CA的延长线上,是否仍能得到∠BQM=60°?
③如果将题中“等边三角形ABC”,改为“等腰直角三角形ABC,且∠BAC=90°”,是否仍能得到∠BQM=60°?
请你作出判断,在下列横线上填写“是”或“否”:①
是
是
;②是
是
;③否
否
;并选择其中一个真命题给出证明.
分析:(1)根据等边三角形性质得出AB=AC,∠ABC=∠C=60°,根据SAS证△ABM≌△BCN,推出∠NBC=∠BAM,求出∠BAM+∠ABN=60°即可;
(2)①根据∠BQM=60°和∠ABC=60°求出∠BAM=∠CBN推出△BCN≌△ABM即可;②求出△ABN≌△CAM,推出∠M=∠N,∠NAQ=∠CAM,根据∠CAM+∠M=∠ACB=60°和∠NAQ=∠CAM求出∠N+∠NAQ=60°即可;③∠BQM=∠ABC=45°.
(2)①根据∠BQM=60°和∠ABC=60°求出∠BAM=∠CBN推出△BCN≌△ABM即可;②求出△ABN≌△CAM,推出∠M=∠N,∠NAQ=∠CAM,根据∠CAM+∠M=∠ACB=60°和∠NAQ=∠CAM求出∠N+∠NAQ=60°即可;③∠BQM=∠ABC=45°.
解答:(1)证明:∵△ABC是等边三角形,
∴AB=AC,∠ABC=∠C=60°
∵在△ABM和△BCN中,
,
∴△ABM≌△BCN,
∴∠NBC=∠BAM,
又∵∠NBC+∠ABN=60°,
∴∠BAM+∠ABN=60°,
即∠BQM=60°;
(2)①是;②是;③否,
选②,
证明:∵△ABC是等边三角形,
∴AB=AC,∠ABC=∠C=∠BAC=60°,
∴∠BAN=∠ACM=120°,
∵CN=BM,BC=AC,
∴AN=CM,
∵在△ABN和△CAM中,
,
∴△ABN≌△CAM,
∴∠M=∠N,∠NAQ=∠CAM,
又∵∠CAM+∠M=∠ACB=60°,∠NAQ=∠CAM,
∴∠N+∠NAQ=60°,
即∠BQM=60°,
故答案为:是,是,否.
∴AB=AC,∠ABC=∠C=60°
∵在△ABM和△BCN中,
|
∴△ABM≌△BCN,
∴∠NBC=∠BAM,
又∵∠NBC+∠ABN=60°,
∴∠BAM+∠ABN=60°,
即∠BQM=60°;
(2)①是;②是;③否,
选②,
证明:∵△ABC是等边三角形,
∴AB=AC,∠ABC=∠C=∠BAC=60°,
∴∠BAN=∠ACM=120°,
∵CN=BM,BC=AC,
∴AN=CM,
∵在△ABN和△CAM中,
|
∴△ABN≌△CAM,
∴∠M=∠N,∠NAQ=∠CAM,
又∵∠CAM+∠M=∠ACB=60°,∠NAQ=∠CAM,
∴∠N+∠NAQ=60°,
即∠BQM=60°,
故答案为:是,是,否.
点评:本题考查了等边三角形的性质,全等三角形的性质和判定,三角形的外角性质的应用.

练习册系列答案
相关题目
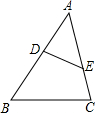 如图,点D、E分别在△ABC的边上AB、AC上,且∠AED=∠ABC,若DE=3,BC=6,AB=8,则AE的长为
如图,点D、E分别在△ABC的边上AB、AC上,且∠AED=∠ABC,若DE=3,BC=6,AB=8,则AE的长为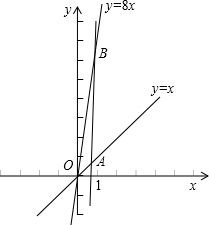 如图,点A,B分别在一次函数y=x,y=8x的图象上,其横坐标分别为a,b (a>0,b>0 ).若直线AB为一次函数y=kx+m的图象,则当
如图,点A,B分别在一次函数y=x,y=8x的图象上,其横坐标分别为a,b (a>0,b>0 ).若直线AB为一次函数y=kx+m的图象,则当 19、如图,点M、N分别在正三角形ABC的BC、CA边上,且BM=CN,AM、BN交于点Q,求∠AQN的度数.
19、如图,点M、N分别在正三角形ABC的BC、CA边上,且BM=CN,AM、BN交于点Q,求∠AQN的度数. 12、如图,点D、E分别在∠BAC的边上,连接DC、BE,若∠B=∠C,那么补充下列一个条件后,仍无法判定△ABE≌△ACD的是( )
12、如图,点D、E分别在∠BAC的边上,连接DC、BE,若∠B=∠C,那么补充下列一个条件后,仍无法判定△ABE≌△ACD的是( ) 如图,点A、B分别在直线l1、l2上,过点A作到l2的距离AM,过点B作直线l3∥l1.
如图,点A、B分别在直线l1、l2上,过点A作到l2的距离AM,过点B作直线l3∥l1.