题目内容
 如图,?ABCD的顶点B在矩形AEFC的边EF上,点B与点E、F不重合.若△ACD的面积为5,则图中的阴影部分两个三角形的面积和为
如图,?ABCD的顶点B在矩形AEFC的边EF上,点B与点E、F不重合.若△ACD的面积为5,则图中的阴影部分两个三角形的面积和为考点:平行四边形的性质,矩形的性质
专题:
分析:根据平行四边形的对角线把平行四边形分成的两个三角形的面积相等求出△ABC的面积,再根据三角形的面积公式和矩形的面积公式求出矩形的面积,然后求解即可.
解答:解:在?ABCD中,∵△ACD的面积为3,
∴△ABC的面积为5,
∴S△ABC=
AC•AE=10,
∴AC•AE=10,
∴矩形AEFC的面积为10,
阴影部分两个三角形的面积和=10-5=5,
故答案为:5.
∴△ABC的面积为5,
∴S△ABC=
| 1 |
| 2 |
∴AC•AE=10,
∴矩形AEFC的面积为10,
阴影部分两个三角形的面积和=10-5=5,
故答案为:5.
点评:本题考查了矩形的性质,平行四边形的性质,根据三角形的面积求出矩形的面积是解题的关键,也是本题的难点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,有一块直角三角形纸片,两直角边AC=5cm,BC=12cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
如图,有一块直角三角形纸片,两直角边AC=5cm,BC=12cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )A、
| ||
| B、3m | ||
C、
| ||
| D、5m |
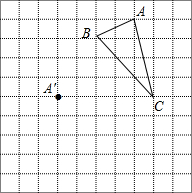 在正方形网格中,△ABC三个顶点的位置都在格点上如图所示,现将△ABC平移,使点A移动到点A′,点B′,点C′分别是B、C的对应点.
在正方形网格中,△ABC三个顶点的位置都在格点上如图所示,现将△ABC平移,使点A移动到点A′,点B′,点C′分别是B、C的对应点. 如图,OA⊥OB,若∠1=40°,则∠2的度数是
如图,OA⊥OB,若∠1=40°,则∠2的度数是 如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线交AC于点E,垂足为点D,连接BE,则∠EBC的度数为
如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线交AC于点E,垂足为点D,连接BE,则∠EBC的度数为