题目内容
已知:一等腰三角形的两边长x,y满足方程组 ,则此等腰三角形的周长为
,则此等腰三角形的周长为
- A.5
- B.4
- C.3
- D.5或4
A
分析:求等腰三角形的周长,即是确定等腰三角形的腰与底的长求周长.首先求出方程组的解,再根据三角形三边关系定理列出不等式,确定是否符合题意.
解答:解方程组 得,
得,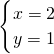 .
.
当腰为2,1为底时,2-1<2<2+1,能构成三角形,周长为2+2+1=5;
当腰为1,2为底时,1+1=2,不能构成三角形.
故选A.
点评:本题从边的方面考查三角形,涉及分类讨论的思想方法.求三角形的周长,不能盲目地将三边长相加起来,而应养成检验三边长能否组成三角形的好习惯,把不符合题意的舍去.
分析:求等腰三角形的周长,即是确定等腰三角形的腰与底的长求周长.首先求出方程组的解,再根据三角形三边关系定理列出不等式,确定是否符合题意.
解答:解方程组
 得,
得,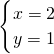 .
.当腰为2,1为底时,2-1<2<2+1,能构成三角形,周长为2+2+1=5;
当腰为1,2为底时,1+1=2,不能构成三角形.
故选A.
点评:本题从边的方面考查三角形,涉及分类讨论的思想方法.求三角形的周长,不能盲目地将三边长相加起来,而应养成检验三边长能否组成三角形的好习惯,把不符合题意的舍去.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
已知:一等腰三角形的两边长x,y满足方程组
,则此等腰三角形的周长为( )
|
| A、5 | B、4 | C、3 | D、5或4 |
 ,则此等腰三角形的周长为 .
,则此等腰三角形的周长为 . ,则此等腰三角形的周长为( )
,则此等腰三角形的周长为( ) ,则此等腰三角形的周长为( )
,则此等腰三角形的周长为( )