题目内容
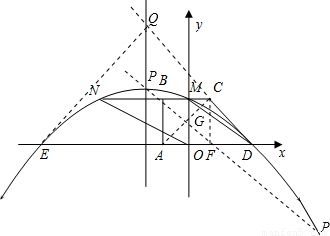
如图所示,在平面直角坐标系中,四边形ABCD是直角梯形,BC∥AD,∠BAD=90°,BC与y轴相交于点M,且M是BC的中点,A、B、D三点的坐标分别是A(-1,0),B(-l,2),D(3,0).连接DM,并把线段DM沿DA方向平移到ON.若抛物线y=ax2+bx+c经过点D、M、N.(1)求抛物线的解析式.
(2)抛物线上是否存在点P,使得PA=PC?若存在,求出点P的坐标;若不存在,请说明理由.
(3)设抛物线与x轴的另一个交点为E,点Q是抛物线的对称轴上的一个动点,当点Q在什么位置时有|QE-QC|最大?并求出最大值.

【答案】分析:(1)根据B点坐标可求M点坐标,根据平移关系可知OD=MN=3,可求N点坐标,将D(3,0),M(0,2),N(-3,2)代入抛物线解析式,列方程组求解;
(2)连接AC交y轴与G,根据M为BC的中点求C的坐标,根据A、B、C三点坐标,判断BG为AC的垂直平分线,求直线BG的解析式,再与抛物线联立,解方程组求满足条件的P点坐标;
(3)由抛物线的对称性可知QE=QD,故当Q、C、D三点共线时,|QE-QC|最大,延长DC与x=- 相交于点Q,先求直线CD的解析式,将x=-
相交于点Q,先求直线CD的解析式,将x=- 代入,可求Q点坐标,过点C作CF⊥x轴,垂足为F,此时,|QE-QC|=CD,在Rt△CDF中求CD即可.
代入,可求Q点坐标,过点C作CF⊥x轴,垂足为F,此时,|QE-QC|=CD,在Rt△CDF中求CD即可.
解答:解:(1)∵BC∥AD,B(-1,2),M是BC与y轴的交点,∴M(0,2),
∵DM∥ON,D(3,0),
∴N(-3,2),
则 ,
,
解得 ,
,
∴y=- x2-
x2- x+2;
x+2;
(2)连接AC交y轴于G,
∵M是BC的中点,
∴AO=BM=MC,AB=BC=2,
∴AG=GC,即G(0,1),
∵∠ABC=90°,
∴BG⊥AC,即BG是AC的垂直平分线,要使PA=PC,即点P在AC的垂直平分线上,故P在直线BG上,
∴点P为直线BG与抛物线的交点,
设直线BG的解析式为y=kx+b,
则 ,
,
解得 ,
,
∴y=-x+1,
∴ ,
,
解得 ,
, ,
,
∴点P(3+3 ,-2-3
,-2-3 )或P(3-3
)或P(3-3 ,-2+3
,-2+3 ),
),
(3)∵y=- x2-
x2- x+2=-
x+2=- (x+
(x+ )2+2
)2+2 ,
,
∴对称轴x=- ,
,
令- x2-
x2- x+2=0,
x+2=0,
解得x1=3,x2=-6,
∴E(-6,0),
故E、D关于直线x=- 对称,
对称,
∴QE=QD,
∴|QE-QC|=|QD-QC|,
要使|QE-QC|最大,则延长DC与x=- 相交于点Q,即点Q为直线DC与直线x=-
相交于点Q,即点Q为直线DC与直线x=- 的交点,
的交点,
由于M为BC的中点,
∴C(1,2),
设直线CD的解析式为y=kx+b,
则 ,
,
解得 ,
,
∴y=-x+3,
当x=- 时,y=
时,y= +3=
+3= ,
,
故当Q在(- ,
, )的位置时,|QE-QC|最大,
)的位置时,|QE-QC|最大,
过点C作CF⊥x轴,垂足为F,
则CD= =
= =2
=2 .
.
点评:本题考查了二次函数的综合运用.关键是根据点的坐标,判断三角形的特殊性,根据抛物线的对称性求满足条件的点.
(2)连接AC交y轴与G,根据M为BC的中点求C的坐标,根据A、B、C三点坐标,判断BG为AC的垂直平分线,求直线BG的解析式,再与抛物线联立,解方程组求满足条件的P点坐标;
(3)由抛物线的对称性可知QE=QD,故当Q、C、D三点共线时,|QE-QC|最大,延长DC与x=-
 相交于点Q,先求直线CD的解析式,将x=-
相交于点Q,先求直线CD的解析式,将x=- 代入,可求Q点坐标,过点C作CF⊥x轴,垂足为F,此时,|QE-QC|=CD,在Rt△CDF中求CD即可.
代入,可求Q点坐标,过点C作CF⊥x轴,垂足为F,此时,|QE-QC|=CD,在Rt△CDF中求CD即可.解答:解:(1)∵BC∥AD,B(-1,2),M是BC与y轴的交点,∴M(0,2),
∵DM∥ON,D(3,0),
∴N(-3,2),
则
 ,
,解得
 ,
,∴y=-
 x2-
x2- x+2;
x+2;(2)连接AC交y轴于G,
∵M是BC的中点,
∴AO=BM=MC,AB=BC=2,
∴AG=GC,即G(0,1),
∵∠ABC=90°,
∴BG⊥AC,即BG是AC的垂直平分线,要使PA=PC,即点P在AC的垂直平分线上,故P在直线BG上,
∴点P为直线BG与抛物线的交点,
设直线BG的解析式为y=kx+b,
则
 ,
,解得
 ,
,∴y=-x+1,
∴
 ,
,解得
 ,
, ,
,∴点P(3+3
 ,-2-3
,-2-3 )或P(3-3
)或P(3-3 ,-2+3
,-2+3 ),
),
(3)∵y=-
 x2-
x2- x+2=-
x+2=- (x+
(x+ )2+2
)2+2 ,
,∴对称轴x=-
 ,
,令-
 x2-
x2- x+2=0,
x+2=0,解得x1=3,x2=-6,
∴E(-6,0),
故E、D关于直线x=-
 对称,
对称,∴QE=QD,
∴|QE-QC|=|QD-QC|,
要使|QE-QC|最大,则延长DC与x=-
 相交于点Q,即点Q为直线DC与直线x=-
相交于点Q,即点Q为直线DC与直线x=- 的交点,
的交点,由于M为BC的中点,
∴C(1,2),
设直线CD的解析式为y=kx+b,
则
 ,
,解得
 ,
,∴y=-x+3,
当x=-
 时,y=
时,y= +3=
+3= ,
,故当Q在(-
 ,
, )的位置时,|QE-QC|最大,
)的位置时,|QE-QC|最大,过点C作CF⊥x轴,垂足为F,
则CD=
 =
= =2
=2 .
.点评:本题考查了二次函数的综合运用.关键是根据点的坐标,判断三角形的特殊性,根据抛物线的对称性求满足条件的点.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 交于点A,过点A分别作x轴、y轴的垂线,垂足为点B、C.如果四边形OBAC是正方形,求一次函数的关系式.
交于点A,过点A分别作x轴、y轴的垂线,垂足为点B、C.如果四边形OBAC是正方形,求一次函数的关系式. 5、如图所示,在平面直角坐标系中,点A、B的坐标分别为(-2,0)和(2,0).月牙①绕点B顺时针旋转90°得到月牙②,则点A的对应点A′的坐标为( )
5、如图所示,在平面直角坐标系中,点A、B的坐标分别为(-2,0)和(2,0).月牙①绕点B顺时针旋转90°得到月牙②,则点A的对应点A′的坐标为( )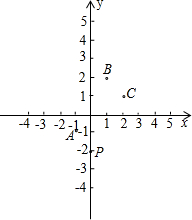 如图所示,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A,B,C作循环对称跳动,即第一次从点P跳到关于点A的对称点M处,第二次从点M跳到关于点B的对称点N处,第三次从点N跳到关于点C的对称点处,…如此下去.
如图所示,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A,B,C作循环对称跳动,即第一次从点P跳到关于点A的对称点M处,第二次从点M跳到关于点B的对称点N处,第三次从点N跳到关于点C的对称点处,…如此下去. 如图所示,在平面直角坐标系xoy中,有一组对角线长分别为1,2,3的正方形A1B1C1O、A2B2C2B1、A3B3C3B2,其对角线OB1、B1B2、B2 B3依次放置在y轴上(相邻顶点重合),依上述排列方式,对角线长为n的第n个正方形的顶点An的坐标为
如图所示,在平面直角坐标系xoy中,有一组对角线长分别为1,2,3的正方形A1B1C1O、A2B2C2B1、A3B3C3B2,其对角线OB1、B1B2、B2 B3依次放置在y轴上(相邻顶点重合),依上述排列方式,对角线长为n的第n个正方形的顶点An的坐标为 BE.
BE.