题目内容
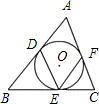 如图,圆O为△ABC内切圆,∠B=40°,∠C=60°,则∠DEF=
如图,圆O为△ABC内切圆,∠B=40°,∠C=60°,则∠DEF=分析:由题意,可证得BE=BD,CE=CF;又∠B=40°,∠C=60°;利用等边对等角,可求得∠DEB和∠FEC的度数;再利用平角为180°,问题即可求出.
解答: 解:∵圆O为△ABC内切圆,BD,BE是切线,
解:∵圆O为△ABC内切圆,BD,BE是切线,
连接OD、OE、OB,则OD⊥BD,OE⊥BE;
∴OD=OE,OB=OB;
∴△BDO≌△BEO,
∴BD=BE;
又∵∠B=40°,
∴∠DEB=∠EDB=
(180°-40°)=70°,
∵∠C=60°,CE,CF是圆的切线,
∴同理可得,∠FEC=∠EFC=
(180°-60°)=60°,
∴∠DEF=180°-∠DEB-∠FEC=180°-70°-60°=50°.
 解:∵圆O为△ABC内切圆,BD,BE是切线,
解:∵圆O为△ABC内切圆,BD,BE是切线,连接OD、OE、OB,则OD⊥BD,OE⊥BE;
∴OD=OE,OB=OB;
∴△BDO≌△BEO,
∴BD=BE;
又∵∠B=40°,
∴∠DEB=∠EDB=
| 1 |
| 2 |
∵∠C=60°,CE,CF是圆的切线,
∴同理可得,∠FEC=∠EFC=
| 1 |
| 2 |
∴∠DEF=180°-∠DEB-∠FEC=180°-70°-60°=50°.
点评:本题综合考查利用圆与三角形的关系来求角的大小,关键是充分利用已知条件:有切线就有垂直关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
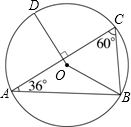 如图,圆O为△ABC的外接圆,其中D点在
如图,圆O为△ABC的外接圆,其中D点在 |
| AC |
| A、132 | B、144 |
| C、156 | D、168 |
 (1997•台湾)已知:如图,圆O′为△ABC之内切圆,圆O′为△ABC之外接圆.
(1997•台湾)已知:如图,圆O′为△ABC之内切圆,圆O′为△ABC之外接圆.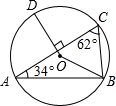 如图,圆O为△ABC的外接圆,其中D点在
如图,圆O为△ABC的外接圆,其中D点在 已知:如图,圆O′为△ABC之内切圆,圆O′为△ABC之外接圆.
已知:如图,圆O′为△ABC之内切圆,圆O′为△ABC之外接圆.