题目内容
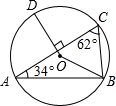 如图,圆O为△ABC的外接圆,其中D点在
如图,圆O为△ABC的外接圆,其中D点在 | AC |
152°
152°
.分析:连接CO,由圆周角定理可求∠BOC,由等腰三角形的性质求∠BCO,可得∠OCA,利用互余关系求∠COD,则∠BOD=∠BOC+∠COD.
解答: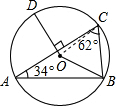 解:连接CO,∠BOC=2∠BAC=2×34°=68°,
解:连接CO,∠BOC=2∠BAC=2×34°=68°,
在△BOC中,
∵BO=CO,
∴∠BCO=(180°-68°)÷2=56°,
∴∠OCA=∠BCA-56°=62°-56°=6°,
又OD⊥AC,
∴∠COD=90°-∠OCA=90°-6°=84°,
∴∠BOD=∠BOC+∠COD=68°+84°=152°.
故答案为:152°.
 解:连接CO,∠BOC=2∠BAC=2×34°=68°,
解:连接CO,∠BOC=2∠BAC=2×34°=68°,在△BOC中,
∵BO=CO,
∴∠BCO=(180°-68°)÷2=56°,
∴∠OCA=∠BCA-56°=62°-56°=6°,
又OD⊥AC,
∴∠COD=90°-∠OCA=90°-6°=84°,
∴∠BOD=∠BOC+∠COD=68°+84°=152°.
故答案为:152°.
点评:本题考查了圆周角定理及三角形内角和定理,解答此题的关键是将圆周角的度数转化为圆心角的度数,利用互余关系,角的和差关系求解.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
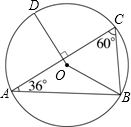 如图,圆O为△ABC的外接圆,其中D点在
如图,圆O为△ABC的外接圆,其中D点在 |
| AC |
| A、132 | B、144 |
| C、156 | D、168 |
 (1997•台湾)已知:如图,圆O′为△ABC之内切圆,圆O′为△ABC之外接圆.
(1997•台湾)已知:如图,圆O′为△ABC之内切圆,圆O′为△ABC之外接圆.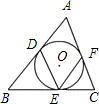 如图,圆O为△ABC内切圆,∠B=40°,∠C=60°,则∠DEF=
如图,圆O为△ABC内切圆,∠B=40°,∠C=60°,则∠DEF= 已知:如图,圆O′为△ABC之内切圆,圆O′为△ABC之外接圆.
已知:如图,圆O′为△ABC之内切圆,圆O′为△ABC之外接圆.