Question

如图,△AEF中,∠EAF=45°,AG⊥EF于点G,现将△AEG沿AE折叠得到△AEB,将△AFG沿AF折叠得到△AFD,延长BE和DF相交于点C．

(1)求证：四边形ABCD是正方形；
(2)连接BD分别交AE、AF于点M、N，将△ABM绕点A逆时针旋转，使AB与AD重合，得到△ADH，试判断线段MN、ND、DH之间的数量关系，并说明理由．(3)若EG=4，GF=6，BM=3，求AG、MN的长．（12分）

Answer 1

（1）可通过矩形中两边相等从而得出该四边形为正方形。
（2）MN²=ND²+DH²  （3）AG=12，MN=5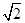

解析试题分析：(1)由∠BAD=∠ABC=∠ADC=90°,得矩形ABCD,
由AB=AD，得四边形ABCD是正方形.
(2)MN²=ND²+DH².
理由：连接NH，由△ABM≌△ADH，得AM=AH，BM=DH，
∠ADH=∠ABD=45°, ∴∠NDH=90°,
再证△AMN≌△AHN，得MN=NH， 
∴MN²=ND²+DH².
(3)设AG=x，则EC=x-4,CF=x-6,
由Rt△ECF，得(x-4)²+(x-6)²=100,x₁=12,x₂=-2(舍去) ∴AG=12.
由AG=AB=AD=12,得BD=12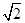,∴MD=9,
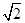设NH=y,由Rt△NHD,得y²=(9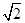-y)²+(3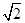)²,y=5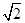,即MN=5.
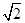考点：四边形的性质和判定及勾股定理
点评：对于证明题，学生可采用逆向思维验证，对于求边相等的，可采用全等三角形，求取边的具体长度的，勾股定理是首要选择。