题目内容
2．设x1，x2是方程2x2-3x-5=0的两个根，利用根与系数的关系，求（1+$\frac{1}{{x}_{1}}$）（1+$\frac{1}{{x}_{2}}$）的值．分析 先根据根与系数的关系得到x1+x2=$\frac{3}{2}$，x1x2=-$\frac{5}{2}$，再把（1+$\frac{1}{{x}_{1}}$）（1+$\frac{1}{{x}_{2}}$）展开变形得到1+$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$+$\frac{1}{{x}_{1}{x}_{2}}$，然后利用代入的方法计算．
解答 解：根据题意得x1+x2=$\frac{3}{2}$，x1x2=-$\frac{5}{2}$，
（1+$\frac{1}{{x}_{1}}$）（1+$\frac{1}{{x}_{2}}$）
=1+$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$+$\frac{1}{{x}_{1}{x}_{2}}$
=1+$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$+$\frac{1}{{x}_{1}{x}_{2}}$
=1+$\frac{\frac{3}{2}}{-\frac{5}{2}}$+$\frac{1}{-\frac{5}{2}}$
=1-$\frac{3}{5}$-$\frac{2}{5}$
=0．
点评 本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-$\frac{b}{a}$，x1x2=$\frac{c}{a}$
练习册系列答案
相关题目
一次函数y=ax+b的图象如图所示，化简|a|+|b|-|a-b|的结果是0．
10．
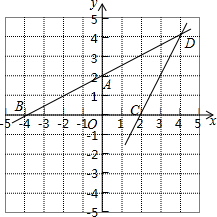如图，直线AB的关系式为0.5x-y=-2，直线CD的关系式为2x-y=4，点D为两条直线的交点，则方程$\left\{\begin{array}{l}{0.5x-y=-2}\\{2x-y=4}\end{array}\right.$的解为（ ）
如图，直线AB的关系式为0.5x-y=-2，直线CD的关系式为2x-y=4，点D为两条直线的交点，则方程$\left\{\begin{array}{l}{0.5x-y=-2}\\{2x-y=4}\end{array}\right.$的解为（ ）| A． | $\left\{\begin{array}{l}{x=0}\\{y=-4}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x=0}\\{y=2}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x=-4}\\{y=0}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x=4}\\{y=4}\end{array}\right.$ |
如图，在平面直角坐标系中，一块等腰直角三角形ABC的直角顶点A在y轴上，坐标为（0，-1），另一顶点B坐标为（-2，0），已知二次函数y=$\frac{3}{2}$x2+bx+c的图象经过B，C两点，过点C作CD⊥y轴，垂足为点D