题目内容
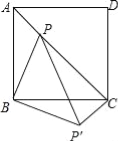
【题目】已知：如图，在
中，
，
为定长，以为直径的
分别交
、
于点
、
.联结
、
.下列结论：①
；②点到的距离不变；③
；④
为外接圆的切线.其中正确的结论是（ ）
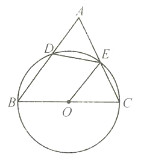
A.①②B.③④C.①②③D.①②④
【答案】A
【解析】
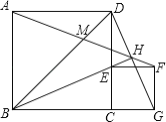
连接OD，可证明△ODE是等边三角形，所以①、②正确；根据已知条件，当AC与
相切时，点C、E重合判断出
，所以③错误；根据切线的定义，④错误.
连接OD，如下图所示：
∵∠A=60°
∴∠B+∠C=120°，
∴
，
∵
，
∴
，
∴
又∵OD=OE
∴△ODE是等边三角形，所以①正确，
则D到OE的长度是等边△ODE的高，则一定是一个定值，因而②正确；
当AC与相切时，点C、E重合，如下图所示：
∵
为直径
∴
∴
又∵此时点C、E重合
∴
∴
∴③不一定成立，故③错误；
根据切线的定义只有在③这种情况下才是切线，其他时候都不是切线，故④错误．
故选：A．
练习册系列答案
相关题目
