Question

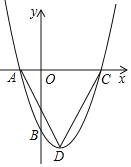
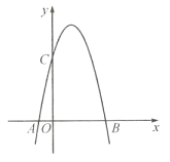
【题目】如图，一个二次函数的图像经过、、三点，点的坐标为，点的坐标为，点在轴的正半轴上，且.

（1）求点的坐标；

（2）求这个二次函数的解析式；

（3）自变量在什么范围内时，随的增大而增大？何时，随的增大而减小

Answer 1

【答案】（1）；（2） ；（3）当自变量时，随的增大而增大，当自变量时，随的增大而减小.

【解析】

（1）先求出AB的长度，再根据得出点的坐标；

（2）根据已知的两点，和（1）中求得的点的坐标列出方程组即可求解；

（3）先得出对称轴，根据二次函数的图像性质判断随的增减变化情况.

（1）由题意得：

∴

∴点的坐标为；

（2）∵点的坐标为

∴可设二次函数的解析式为：

∴

解得：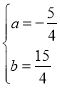

∴二次函数的解析式为：；

（3）由题可得该二次函数的对称轴为

∵时，随的增大而增大，当自变量时，随的增大而减小.