题目内容
把一条长为1.35m的铁丝弯成顶角为150°的等腰三角形,求此三角形的各边长.
考点:勾股定理的应用,等腰三角形的性质
专题:
分析:设等腰三角形为△ABC,∠A=150°,∠B=∠C=15°,构造等腰三角形CBD和等腰三角形AHD来解答.
解答: 解:如图:设等腰三角形为△ABC,∠A=150°,∠B=∠C=15°,设AB=AC=x,BC=y
解:如图:设等腰三角形为△ABC,∠A=150°,∠B=∠C=15°,设AB=AC=x,BC=y
延长CA至D点使∠BDC=15°
∴BD=BC=y
过D作DH⊥AB于H
有∠DAB=30°,∠DBH=∠HDB=45°
所以DH=BH=
y
在△DHA中,
×
y=
y+x,又有2x+y=1.35,
解得x=0.343,y=0.663.
 解:如图:设等腰三角形为△ABC,∠A=150°,∠B=∠C=15°,设AB=AC=x,BC=y
解:如图:设等腰三角形为△ABC,∠A=150°,∠B=∠C=15°,设AB=AC=x,BC=y延长CA至D点使∠BDC=15°
∴BD=BC=y
过D作DH⊥AB于H
有∠DAB=30°,∠DBH=∠HDB=45°
所以DH=BH=
| ||
| 2 |
在△DHA中,
| 3 |
| ||
| 2 |
| ||
| 2 |
解得x=0.343,y=0.663.
点评:本题考查了等腰三角形的性质和解直角三角形,作出适当辅助线是解题的关键.

练习册系列答案
相关题目
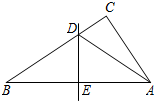 如图:Rt△ABC中,∠C=90°,AB的垂直平分线DE交AB、BC于E、D.
如图:Rt△ABC中,∠C=90°,AB的垂直平分线DE交AB、BC于E、D.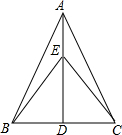 已知如图,AB=AC,AD平分∠BAC,E是AD上一点,求证:
已知如图,AB=AC,AD平分∠BAC,E是AD上一点,求证: