题目内容
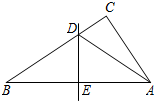 如图:Rt△ABC中,∠C=90°,AB的垂直平分线DE交AB、BC于E、D.
如图:Rt△ABC中,∠C=90°,AB的垂直平分线DE交AB、BC于E、D.(1)如果AC=6cm,BC=8cm,试求△ACD的周长.
(2)如果∠CAD:∠BAD=4:7,求∠B的度数.
考点:线段垂直平分线的性质,勾股定理
专题:
分析:(1)由AB的垂直平分线DE交AB、BC于E、D,可得AD=BD,继而可得△ACD的周长=AC+BC;
(2)由∠CAD:∠BAD=4:7,可设∠CAD=4x°,∠BAD=7x°,继而可得方程4x+7x+7x=90,解此方程即可求得答案.
(2)由∠CAD:∠BAD=4:7,可设∠CAD=4x°,∠BAD=7x°,继而可得方程4x+7x+7x=90,解此方程即可求得答案.
解答:解:(1)∵AB的垂直平分线是DE,
∴AD=BD,
∵AC=6cm,BC=8cm,
∴△ACD的周长为:AC+CD+AD=AC+BD+CD=AC+BC=14(cm);
(2)∵∠CAD:∠BAD=4:7,
∴设∠CAD=4x°,∠BAD=7x°,
∵AD=BD,
∴∠B=∠BAD=7x°,
∵Rt△ABC中,∠C=90°,
∴∠CAD+∠BAD+∠B=90°,
∴4x+7x+7x=90,
解得:x=5,
∴∠B=35°.
∴AD=BD,
∵AC=6cm,BC=8cm,
∴△ACD的周长为:AC+CD+AD=AC+BD+CD=AC+BC=14(cm);
(2)∵∠CAD:∠BAD=4:7,
∴设∠CAD=4x°,∠BAD=7x°,
∵AD=BD,
∴∠B=∠BAD=7x°,
∵Rt△ABC中,∠C=90°,
∴∠CAD+∠BAD+∠B=90°,
∴4x+7x+7x=90,
解得:x=5,
∴∠B=35°.
点评:此题考查了线段垂直平分线的性质以及等腰三角形的性质.此题难度适中,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
某种商品的进价为1200元,标价为1575元,后来由于该商品积压,商店准备打折出售,但要保持利润不低于5%,则至多可打( )
| A、6折 | B、7折 | C、8折 | D、9折 |
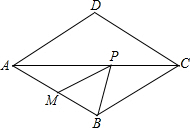 如图,点P是边长为4的菱形ABCD对角线AC上的一个动点,∠BAD=60°,点M是AB边上的中点,求:
如图,点P是边长为4的菱形ABCD对角线AC上的一个动点,∠BAD=60°,点M是AB边上的中点,求: