题目内容
【题目】在平面直角坐标系中,抛物线y=ax2﹣5ax+4a与x轴交于A、B(A点在B点的左侧)与y轴交于点C.
(1)如图1,连接AC、BC,若△ABC的面积为3时,求抛物线的解析式;
(2)如图2,点P为第四象限抛物线上一点且在直线BC下方,连接PC,若∠BCP=2∠ABC时,求点P的横坐标;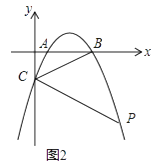
(3)如图3,在(2)的条件下,点F在AP上,过点P作PH⊥x轴于H点,点K在PH的延长线上,AK=KF,∠KAH=∠FKH,PF=﹣4 ![]() a,连接KB并延长交抛物线于点Q,求PQ的长.
a,连接KB并延长交抛物线于点Q,求PQ的长.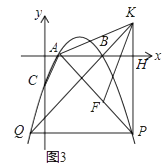
【答案】
(1)解:当y=0时,ax2﹣5ax+4a=0,解得x1=1,x2=4,则A(1,0),B(4,0),
∴AB=3,
∵△ABC的面积为3,
∴ ![]() 3OC=3,解得OC=2,则C(0,﹣2),
3OC=3,解得OC=2,则C(0,﹣2),
把C(0,﹣2)代入y=ax2﹣5ax+4a得4a=﹣2,解得a=﹣ ![]() ,
,
∴抛物线的解析式为y=﹣ ![]() x2+
x2+ ![]() x﹣2;
x﹣2;
(2)解:过点P作PH⊥x轴于H,作CD⊥PH于点H,如图2,设P(x,ax2﹣5ax+4a),则PD=4a﹣(ax2﹣5ax+4a)=﹣ax2+5ax,
∵AB∥CD,
∴∠ABC=∠BCD,
∵∠BCP=2∠ABC,
∴∠PCD=∠ABC,
∴Rt△PCD∽Rt△CBO,
∴PD:OC=CD:OB,
即(﹣ax2+5ax):(﹣4a)=x:4,解得x1=0,x2=6,
∴点P的横坐标为6;
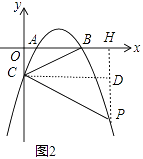
(3)解:过点F作FG⊥PK于点G,如图3,
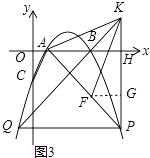
∵AK=FK,
∴∠KAF=∠KFA,
而∠KAF=∠KAH+∠PAH,∠KFA=∠PKF+∠KPF,
∵∠KAH=∠FKP,
∴∠HAP=∠KPA,
∴HA=HP,
∴△AHP为等腰直角三角形,
∵P(6,10a),
∴﹣10a=6﹣1,解得a=﹣ ![]() ,
,
在Rt△PFG中,∵PF=﹣4 ![]() a=2
a=2 ![]() ,∠FPG=45°,
,∠FPG=45°,
∴FG=PG= ![]() PF=2,
PF=2,
在△AKH和△KFG中
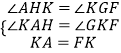 ,
,
∴△AKH≌△KFG,
∴KH=FG=2,
∴K(6,2),
设直线KB的解析式为y=mx+n,
把K(6,2),B(4,0)代入得 ![]() ,
,
解得 ![]() ,
,
∴直线KB的解析式为y=x﹣4,
当a=﹣ ![]() 时,抛物线的解析式为y=﹣
时,抛物线的解析式为y=﹣ ![]() x2+
x2+ ![]() x﹣2,
x﹣2,
解方程组 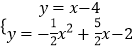 ,
,
解得 ![]() 或
或 ![]() ,
,
∴Q(﹣1,﹣5),
而P(6,﹣5),
∴PQ∥x 轴,
∴QP=7.
【解析】(1)观察函数解析式的特点,求出此函数图像与x轴的交点A、B的坐标,注意:A点在B点的左侧,用待定系数法就可以求出此函数解析式。
(2)根据已知添加辅助线,过点P作PH⊥x轴于H,作CD⊥PH于点H,易证得Rt△PCD∽Rt△CBO,得出对应边成比例,抓住点P在第四象限,设点P的坐标,建立方程,求解即可求出点P的坐标。
(3)过点F作FG⊥PK于点G,先证∠HAP=∠KPA得到HA=HP,根据点P的坐标即可求出a的值,就可以证得△AHP为等腰直角三角形,再证明△AKH≌△KFG,得出KH=FG,即可得到点K的坐标,再求出直线KB的解析式,两函数图像交于点Q,因此由两函数解析式联立方程,求解即可求得Q点坐标,即可求得QP的值。
【考点精析】本题主要考查了确定一次函数的表达式和相似三角形的判定与性质的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.

 阅读快车系列答案
阅读快车系列答案