题目内容
如图,四边形ABCD中,AC⊥BD交BD于点E,点F,M分别是AB,BC的中点,BN平分∠ABE交AM于点N,AB=AC=BD.连接MF,NF.
(1)判断△BMN的形状,并证明你的结论;
(2)判断△MFN与△BDC之间的关系,并说明理由.

(1)答:△BMN是等腰直角三角形.
证明:∵AB=AC,点M是BC的中点,
∴AM⊥BC,AM平分∠BAC.
∵BN平分∠ABE,AC⊥BD,
∴∠AEB=90°,
∴∠EAB+∠EBA=90°,
∴∠MNB=∠NAB+∠ABN=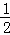 (∠BAE+∠ABE)=45°.
(∠BAE+∠ABE)=45°.
∴△BMN是等腰直角三角形;
(2)答:△MFN∽△BDC.
证明:∵点F,M分别是AB,BC的中点,
∴FM∥AC,FM=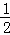 AC.
AC.
∵AC=BD,
∴FM=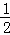 BD,即
BD,即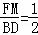 .
.
∵△BMN是等腰直角三角形,
∴NM=BM=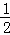 BC,即
BC,即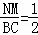 ,
,
∴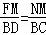 .
.
∵AM⊥BC,
∴∠NMF+∠FMB=90°.
∵FM∥AC,
∴∠ACB=∠FMB.
∵∠CEB=90°,
∴∠ACB+∠CBD=90°.
∴∠CBD+∠FMB=90°,
∴∠NMF=∠CBD.
∴△MFN∽△BDC.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
如图,直线a∥b,射线DC与直线a相交于点C,过点D作DE⊥b于点E,已知∠1=25°,则∠2的度数为( )

|
| A. | 115° | B. | 125° | C. | 155° | D. | 165° |
如图,桌面上有一个一次性纸杯,它的正视图应是( )

|
| A. |
| B. |
| C. |
| D. |
|
关于x的方程m(x+h)2+k=0(m,h,k均为常数,m≠0)的解是x1=﹣3,x2=2,则方程m(x+h﹣3)2+k=0的解是( )
|
| A. | x1=﹣6,x2=﹣1 | B. | x1=0,x2=5 | C. | x1=﹣3,x2=5 | D. | x1=﹣6,x2=2 |
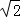 ,2
,2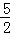 ,CD=4,则弦EF的长为( )
,CD=4,则弦EF的长为( )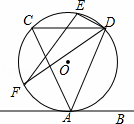
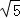 C. 5 D. 6
C. 5 D. 6 •
• .
.