题目内容
 如图,P是正方形对角线上一点,PE⊥BC,PF⊥DC,求证:
如图,P是正方形对角线上一点,PE⊥BC,PF⊥DC,求证:(1)AP=EF;
(2)AP⊥EF.
考点:正方形的性质,全等三角形的判定与性质
专题:证明题
分析:(1)延长FP交AB于点G,通过SAS证明△AGP≌△FPE,根据全等三角形的性质即可得出结论;
(2)延长AP交EF于H.根据全等三角形的性质可得∠GPG=∠FEP,再根据等量关系可得∠PHE=90°,从而证明结论.
(2)延长AP交EF于H.根据全等三角形的性质可得∠GPG=∠FEP,再根据等量关系可得∠PHE=90°,从而证明结论.
解答:证明:(1)延长FP交AB于点G,则PG⊥AB,四边形BEPG是矩形.
∵点P是正方形ABCD的对角线上一点,
∴∠PBG=∠PBE=45°,∠GAE=90°,BC=AB,
又∵PG⊥AB,PE⊥BC,
∴PG=BG=PE,
∴四边形BEPG为正方形,
∴∠GPE=90°,
∴AG=FP.
在△AGP与△FPE中,
,
∴△AGP≌△FPE(SAS),
∴AP=EF;
(2)延ADP交EF于H.
由(1)知△AGP≌△FPE,
∴∠APG=∠FEP,
∵∠APG+∠EPH=180°-∠GPE=90°,
∴∠FEP+∠EPH=90°,
∴∠PHE=90°,即PD⊥EF.

∵点P是正方形ABCD的对角线上一点,
∴∠PBG=∠PBE=45°,∠GAE=90°,BC=AB,
又∵PG⊥AB,PE⊥BC,
∴PG=BG=PE,
∴四边形BEPG为正方形,
∴∠GPE=90°,
∴AG=FP.
在△AGP与△FPE中,
|
∴△AGP≌△FPE(SAS),
∴AP=EF;
(2)延ADP交EF于H.
由(1)知△AGP≌△FPE,
∴∠APG=∠FEP,
∵∠APG+∠EPH=180°-∠GPE=90°,
∴∠FEP+∠EPH=90°,
∴∠PHE=90°,即PD⊥EF.

点评:此题考查了正方形的性质,全等三角形的判定与性质,本题关键是证明△AGP≌△FPE.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
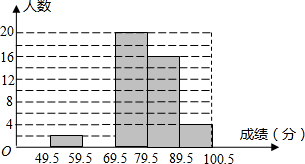 某校初一数学兴趣小组成员小华对本班上期期末考试数学成绩(成绩取整数,满分为100分)作了统计分析,绘制成如下频数分布表和频数分布直方图:
某校初一数学兴趣小组成员小华对本班上期期末考试数学成绩(成绩取整数,满分为100分)作了统计分析,绘制成如下频数分布表和频数分布直方图: 如图,在10×6的正方形网格中,每个小正方形的边长均为单位1,将△ABC向右平移5个单位,得到△A′B′C′,再把△A′B′C′绕点A′顺时针旋转90°,得到△A″B″C″,请你画出△A′B′C′和△A″B″C″(不要求写画法).
如图,在10×6的正方形网格中,每个小正方形的边长均为单位1,将△ABC向右平移5个单位,得到△A′B′C′,再把△A′B′C′绕点A′顺时针旋转90°,得到△A″B″C″,请你画出△A′B′C′和△A″B″C″(不要求写画法).