题目内容
12.已知直线l与⊙O,AB是⊙O的直径,AD⊥l于点D.(1)如图1,当直线l与⊙O相切于点C时,若∠DAC=30°,求∠BAC的大小;
(2)如图2,当直线l与⊙O相交于点E,F时,若∠BAF=18°,求∠DAE的大小.

分析 (1)连接OC,如图1,根据切线的性质得OC⊥CD,则AD∥OC,根据平行线的性质得∠OCA=∠DAC=30°,然后利用等腰三角形的性质可得∠BAC=∠OCA=30°;
(2)连接BF,如图2,根据圆周角定理得到∠AFB=90°,则利用互余得到∠B=72°,再利用圆内接四边形道的性质得∠AED=∠B=72°,然后利用互余计算∠DAE的度数.
解答 解:(1)连接OC,如图1,
∵CD为切线,
∴OC⊥CD,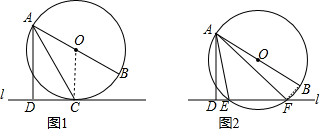
∵AD⊥CD,
∴AD∥OC,
∴∠OCA=∠DAC=30°,
∵OA=OC,
∴∠BAC=∠OCA=30°;
(2)连接BF,如图2,
∵AB为直径,
∴∠AFB=90°,
∴∠B=90°-∠BAF=90°-18°=72°,
∵四边形ABFE为⊙O的内接四边形,
∴∠AED=∠B=72°,
∵AD⊥DE,
∴∠DAE=90°-∠AED=18°.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径;若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.

练习册系列答案
相关题目
2.下列各数中是负分数的是( )
| A. | -3 | B. | $\frac{1}{2}$ | C. | $-\frac{2}{3}$ | D. | 0 |
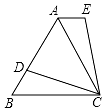 如图,在等边△ABC中,点D是 AB边上一点,连接CD,将线段CD绕点C按顺时针方向旋转60°后得到CE,连接AE.
如图,在等边△ABC中,点D是 AB边上一点,连接CD,将线段CD绕点C按顺时针方向旋转60°后得到CE,连接AE.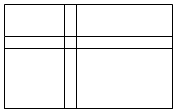 在长为am,宽为bm的一块草坪上修两条互相垂直且宽度都是1m的笔直小路,则余下草坪的面积可表示为(ab-a-b+1)m2.
在长为am,宽为bm的一块草坪上修两条互相垂直且宽度都是1m的笔直小路,则余下草坪的面积可表示为(ab-a-b+1)m2. 有理数a、b在数轴的对应点如图所示,则a+b<0.
有理数a、b在数轴的对应点如图所示,则a+b<0. 根据如图所示的规律.a的值为162.
根据如图所示的规律.a的值为162.