题目内容
有一架梯子，长为2.5米，靠在垂直的墙上，梯子底部离墙的底部0.7米，若梯子顶端下滑了0.4米，则此时梯子底部离墙的底部________米远．
1.5
分析：此题是一个典型的勾股定理实际问题，将梯子看作斜边，将梯子底部离墙的底部看作直角边，列方程解答即可．
解答：首先根据勾股定理求得第一次梯子的高度是
=
=
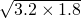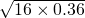=2.4米，
则第二次梯子的高度是2.4-0.4=2，由于梯子的长度不变，根据勾股定理，
得此时梯子底部离墙的底部是
=1.5米．
点评：连续两次运用了勾股定理进行计算，特别注意此题中梯子的长度保持不变．
分析：此题是一个典型的勾股定理实际问题，将梯子看作斜边，将梯子底部离墙的底部看作直角边，列方程解答即可．
解答：首先根据勾股定理求得第一次梯子的高度是
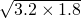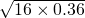===2.4米，则第二次梯子的高度是2.4-0.4=2，由于梯子的长度不变，根据勾股定理，
得此时梯子底部离墙的底部是
=1.5米．点评：连续两次运用了勾股定理进行计算，特别注意此题中梯子的长度保持不变．
练习册系列答案
相关题目
如图，学校的保管室里，有一架5米长的梯子斜靠在墙上，此时梯子与地面所成角为45°，如果梯子底端O固定不动，顶端靠到对面墙上，此时梯子与地面所成的角为60°，则此保管室的宽度AB为（ ）A、
| ||||||
B、
| ||||||
C、3
| ||||||
D、
|
（
+1）米
（
+
）米
米
（
+1）米