��Ŀ����
����Ŀ�����Ƕ��壺����ƽ���͵��ڵ�����ƽ����2���������ν������������Σ�
���磺ij���������߳��ֱ���2��4��![]() ����Ϊ
����Ϊ![]() ��������������������������Σ�
���������������������������
��1�����ݶ��壺���ȱ������������������Ρ����������______���⣨��桱�����⡱����
��2����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ����
����![]() ��������������
��������������![]() ��
��
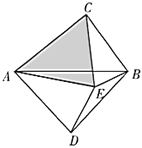
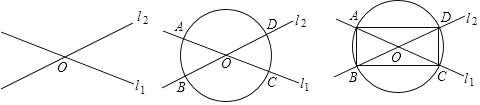
��3����ͼ����![]() Ϊб�߷ֱ���
Ϊб�߷ֱ���![]() ��������ֱ�������Σ���
��������ֱ�������Σ���![]() �����ı���
�����ı���![]() �ڴ��ڵ�
�ڴ��ڵ�![]() ��ʹ��
��ʹ��![]() ��
��![]() ��
��
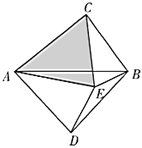
����֤��![]() �����������Σ�
������������
�ڵ�![]() ��ֱ��������ʱ����
��ֱ��������ʱ����![]() �Ķ�����
�Ķ�����
���𰸡���1���棻��2��![]() ����3����֤������������
����3����֤������������![]() ��
��![]() ��
��
��������
��1����ȱ������εı߳�Ϊa����a2+a2=2a2�����ɵó����ۣ�
��2���ɹ��ɶ����ó�a2+b2=c2�٣���Rt��ABC�����������Σ���b��a���ó�a2+c2=2b2�ڣ��ɢ٢ڵó�b=![]() a��c=
a��c=![]() a�����ɵó����ۣ�
a�����ɵó����ۣ�
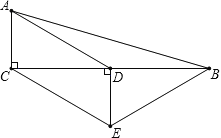
��3�����ɹ��ɶ����ó�AC2+BC2=AB2��AD2+BD2=AB2������֪�ó�2AD2=AB2��AC2+CE2=2AE2�����ɵó���ACE�����������Σ�
������ACE�����������Σ��ó�AC2+CE2=2AE2���������������ֱ�������κ����������ε����ʼ��ɵó��𰸣�
��1���⣺���ȱ�����������������������������������⣬�������£�
��ȱ������ε�һ��Ϊ![]() ����
����![]() ��
��
������������������Ķ��壮
��2���⣺��![]() ����
����![]() �٣�
�٣�
��![]() ��������������
��������������![]() ��
��
��![]() �ڣ�
�ڣ�
�ɢ٢ڵã�![]() ��
��![]() ��
��
��![]() ��
��
��3����֤������![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ������������
������������
���ɢٿɵ�![]() �����������Σ�
������������
��![]() ��
��
��![]() ��ֱ��������ʱ��
��ֱ��������ʱ��
�ɣ�2���ã�![]() ��
��![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ����
����
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��