Question

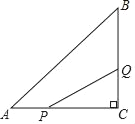
【题目】如图，在△ABC中，∠C＝90°，AC＝8cm，BC＝6cm，点P从点A沿AC向C以2cm/s的速度移动，到C即停，点Q从点C沿CB向B以1cm/s的速度移动，到B就停．

（1）若P、Q同时出发，经过几秒钟S△PCQ＝2cm2；

（2）若点Q从C点出发2s后点P从点A出发，再经过几秒△PCQ与△ACB相似．

Answer 1

【答案】（1）则P、Q同时出发，经过（2±）秒钟S△PCQ=2cm2；（2）点Q从C点出发2s后点P从点A出发，再经过1.6秒或秒秒△PCQ与△ACB相似．

【解析】

（1）根据题意用t表示出CQ，PC，根据三角形的面积公式列出方程，解方程即可；

（2）分△PCQ∽△ACB，△PCQ∽△BCA两种情况列出比例式，计算即可．

（1）由题意得：AP=2t，CQ=t，则PC=8﹣2t，由题意得：×（8﹣2t）×t=2，整理得：t2﹣4t+2=0，解得：t=2±，则P、Q同时出发，经过（2±）秒钟S△PCQ=2cm2；

（2）由题意得：AP=2t，CQ=2+t，则PC=8﹣2t，分两种情况讨论：

①当△PCQ∽△ACB时，=，即=，解得：t=1.6；

②当△PCQ∽△BCA时，=，即=，解得：t=．

综上所述：点Q从C点出发2s后点P从点A出发，再经过1.6秒或秒秒△PCQ与△ACB相似．