题目内容
将抛物线y=2（x-1）2-2绕顶点旋转180°，所得抛物线的解析式是 ．
考点：二次函数图象与几何变换
专题：
分析：将其绕顶点旋转180°后，开口大小和顶点坐标都没有变化，变化的只是开口方向，可据此得出所求的结论．
解答：解：将抛物线y=2（x-1）2-2绕顶点旋转180°后，得：y=-2（x-1）2-2．
故答案为：y=-2（x-1）2-2．
故答案为：y=-2（x-1）2-2．
点评：本题考查了二次函数图象的旋转变换，在绕抛物线顶点旋转过程中，二次函数的开口大小和顶点坐标都没有变化．
练习册系列答案
相关题目
如图，OA=OB，OC=OD，∠O=50°，∠D=35°，则∠DAC等于（ ）| A、60° | B、50° |
| C、85° | D、30° |
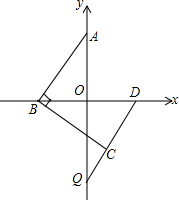已知如图在平面直角坐标系中，点A（0，m），点D（n，0），若|m-a|+（n-b）2=0，a=b．在x轴的负半轴上有一动点B，连接AB，过点B作BC⊥AB，且BC=AB，连接DC并延长交y轴于点Q，试问当B点运动时，点Q的位置是否发生变化？请先作出判断，然后证明你的结论．函数y=
x2+1与y=
x2+2的图象的不同之处是（ ）
| 1 |
| 2 |
| 1 |
| 2 |
| A、对称轴 | B、开口方向 |
| C、顶点 | D、形状 |
若点P（a，-b）在第三象限，则点M（a，-ab）在（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |