Question

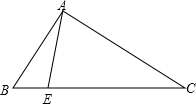
如图已知在Rt△ABC中，∠BAC=90°，E在斜边BC上，CE=CA，求证：∠BAE=

1

2

∠ACB．

Answer 1

证明：∵在Rt△ABC中，∠BAC=90°，
∴∠BAE=90°-∠CAE，
∵CE=CA，
∴∠CAE=

1

2

（180°-∠ACB），
∴∠BAE=90°-∠CAE=90°-

1

2

（180°-∠ACB）=

1

2

∠ACB．