题目内容
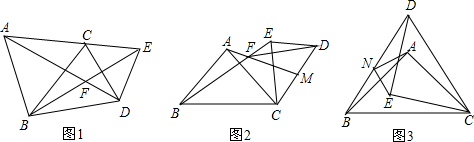
(1)如图1,在△ABC和△ECD是等边△,则BE、AD之间的数量关系为 ;∠DFE度数为 ;请用旋转的性质说明上述关系成立的理由.
(2)如图2,在△ABC和△ECD都是等腰直角三角形,∠BAC=∠CED=90°,M是CD的中点,连AM、BE交于F点,则BE、AM之间的数量关系为 ;∠MFE度数是 ;
(3)如图3,在△ABC和△ECD都是等腰直角三角形,∠BAC=∠CED=90°,N是BD的中点,连AN、NB,则AN、NE有何关系并证明你的结论.
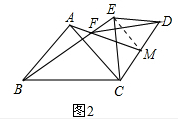
(2)如图2,在△ABC和△ECD都是等腰直角三角形,∠BAC=∠CED=90°,M是CD的中点,连AM、BE交于F点,则BE、AM之间的数量关系为
(3)如图3,在△ABC和△ECD都是等腰直角三角形,∠BAC=∠CED=90°,N是BD的中点,连AN、NB,则AN、NE有何关系并证明你的结论.

考点:全等三角形的判定与性质,等边三角形的性质,等腰直角三角形
专题:
分析:(1)易证△ACD是△BCE顺时针旋转60°来的,可得△ACD≌△BCE,可得∠CAD=∠CBE,即可求得∠DFE=60°;
(2)连接EM,则△CEM是等腰直角三角形,易证∠BCE=∠ACM,
=
,即可证明△BCE∽△ACM,可得
=
=
和∠CBE=∠CAM,即可求得∠MFE=45°;
(3)取BC中点F,取CD中点M,连接MN,AF,NF,EM,易证NF=EM,NM=AF,∠AFN=∠EMN,即可证明△AFN≌△NME,可得AN=EN,∠NAF=∠ENM,即可求得∠ENM+∠ANM=90°,即可解题.
(2)连接EM,则△CEM是等腰直角三角形,易证∠BCE=∠ACM,
| BC |
| AC |
| CE |
| CM |
| BE |
| AM |
| BC |
| AC |
| 2 |
(3)取BC中点F,取CD中点M,连接MN,AF,NF,EM,易证NF=EM,NM=AF,∠AFN=∠EMN,即可证明△AFN≌△NME,可得AN=EN,∠NAF=∠ENM,即可求得∠ENM+∠ANM=90°,即可解题.
解答:解:(1)∵△ABC和△ECD是等边△,
∴∠ACB=∠DCE=60°,
∴∠BCD=60°,
∴△ACD是△BCE顺时针旋转60°来的,
∴△ACD≌△BCE,
∴BE=AD,
∴∠CAD=∠CBE,
∴∠DFE=∠CAD+∠CEB=∠CBE+∠CEF=∠ACB=60°;
故答案为 BE=AD,∠DFE=60°;
(2)连接EM,则△CEM是等腰直角三角形,
∴CE=
CM,∵∠ACB=45°=∠ECM,
∴∠BCE=∠ACM,
∵BC=
AC,
∴
=
=
,
∴△BCE∽△ACM,
∴
=
=
,
∠CBE=∠CAM,
∵∠BFM=∠BAF+∠ABF=∠BAC+∠CAM+∠ABF=90°+∠CBE+∠ABF=90°+∠ABC=135°,
∴∠MFE=45°;
故答案为
,45°;
(3)取BC中点F,取CD中点M,连接MN,AF,NF,EM,
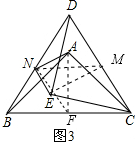
∴NF,NM是△BCD的中位线,
∴NF=
CD=EM,NM=
BC=AF,
∵NF∥CD,NM∥BC,
∴四边形NFCM是平行四边形,
∴∠NFC=∠NMC,
∵∠AFC=90°=∠EMC,∴∠AFN=∠EMN,
∵在△AFN和△NME中,
,
∴△AFN≌△NME,(SAS)
∴AN=EN,∠NAF=∠ENM,
∵MN∥BC,AF⊥BC,
∴MN⊥AF,
∴∠NAF+∠ANM=90°,
∴∠ENM+∠ANM=90°,即∠ANE=90°,
∴AN⊥EN.
∴∠ACB=∠DCE=60°,
∴∠BCD=60°,
∴△ACD是△BCE顺时针旋转60°来的,
∴△ACD≌△BCE,
∴BE=AD,
∴∠CAD=∠CBE,
∴∠DFE=∠CAD+∠CEB=∠CBE+∠CEF=∠ACB=60°;
故答案为 BE=AD,∠DFE=60°;
(2)连接EM,则△CEM是等腰直角三角形,

∴CE=
| 2 |
∴∠BCE=∠ACM,
∵BC=
| 2 |
∴
| BC |
| AC |
| 2 |
| CE |
| CM |
∴△BCE∽△ACM,
∴
| BE |
| AM |
| BC |
| AC |
| 2 |
∠CBE=∠CAM,
∵∠BFM=∠BAF+∠ABF=∠BAC+∠CAM+∠ABF=90°+∠CBE+∠ABF=90°+∠ABC=135°,
∴∠MFE=45°;
故答案为
| 2 |
(3)取BC中点F,取CD中点M,连接MN,AF,NF,EM,

∴NF,NM是△BCD的中位线,
∴NF=
| 1 |
| 2 |
| 1 |
| 2 |
∵NF∥CD,NM∥BC,
∴四边形NFCM是平行四边形,
∴∠NFC=∠NMC,
∵∠AFC=90°=∠EMC,∴∠AFN=∠EMN,
∵在△AFN和△NME中,
|
∴△AFN≌△NME,(SAS)
∴AN=EN,∠NAF=∠ENM,
∵MN∥BC,AF⊥BC,
∴MN⊥AF,
∴∠NAF+∠ANM=90°,
∴∠ENM+∠ANM=90°,即∠ANE=90°,
∴AN⊥EN.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中构建并求证△AFN≌△NME是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
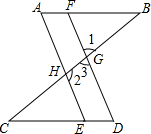 如图,∠1+∠2=180°,∠A=∠D.求证:∠B=∠C.
如图,∠1+∠2=180°,∠A=∠D.求证:∠B=∠C. 如图,∠AMB=90°,∠CMD=90°,ME、MF分别是射线MA、MD的反向延长线.
如图,∠AMB=90°,∠CMD=90°,ME、MF分别是射线MA、MD的反向延长线. 已知△ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B,C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB、AC于点F、G,连接BE.
已知△ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B,C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB、AC于点F、G,连接BE.
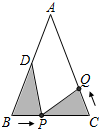 如图,在△ABC中,AB=AC=12,BC=8,D为AB的中点,点P在线段BC上以每秒2个单位的速度由B点向C点运动,同时,点Q在线段CA上以每秒x个单位的速度由C点向A点运动.当△BPD与以C、Q、P为顶点的三角形全等时,x的值为
如图,在△ABC中,AB=AC=12,BC=8,D为AB的中点,点P在线段BC上以每秒2个单位的速度由B点向C点运动,同时,点Q在线段CA上以每秒x个单位的速度由C点向A点运动.当△BPD与以C、Q、P为顶点的三角形全等时,x的值为