题目内容
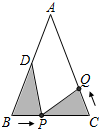 如图,在△ABC中,AB=AC=12,BC=8,D为AB的中点,点P在线段BC上以每秒2个单位的速度由B点向C点运动,同时,点Q在线段CA上以每秒x个单位的速度由C点向A点运动.当△BPD与以C、Q、P为顶点的三角形全等时,x的值为
如图,在△ABC中,AB=AC=12,BC=8,D为AB的中点,点P在线段BC上以每秒2个单位的速度由B点向C点运动,同时,点Q在线段CA上以每秒x个单位的速度由C点向A点运动.当△BPD与以C、Q、P为顶点的三角形全等时,x的值为考点:全等三角形的判定
专题:动点型
分析:求出BD,根据全等得出要使△BPD与△CQP全等,必须BD=CP或BP=CP,得出方程12=16-4x或4x=16-4x,求出方程的解即可.
解答:解:设经过t秒后,使△BPD与△CQP全等,
∵AB=AC=12,点D为AB的中点,
∴BD=6,
∵∠ABC=∠ACB,
∴要使△BPD与△CQP全等,必须BD=CP或BP=CP,
即6=8-2t或2t=8-2t,
t1=1,t2=2,
t=1时,BP=CQ=2,2÷1=2;
t=2时,BD=CQ=6,6÷2=3;
即点Q的运动速度是2或3,
故答案为:2或3.
∵AB=AC=12,点D为AB的中点,
∴BD=6,
∵∠ABC=∠ACB,
∴要使△BPD与△CQP全等,必须BD=CP或BP=CP,
即6=8-2t或2t=8-2t,
t1=1,t2=2,
t=1时,BP=CQ=2,2÷1=2;
t=2时,BD=CQ=6,6÷2=3;
即点Q的运动速度是2或3,
故答案为:2或3.
点评:本题考查了全等三角形的判定的应用,关键是能根据题意得出方程.

练习册系列答案
相关题目
下列各式中一元一次方程的个数有( )
①2x-52;②
=1;③2x+y=5;④3x=2x-1;⑤x=1.
①2x-52;②
| 1 |
| x |
| A、0个 | B、1个 | C、2个 | D、3个 |
计算
+
+
的结果是( )
| 1 |
| x-2 |
| 2 |
| x+2 |
| 4 |
| 4-x2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
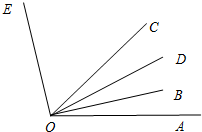 如图,∠EOD=70°,射线OC、OB是∠EOA、∠DOA的角平分线.
如图,∠EOD=70°,射线OC、OB是∠EOA、∠DOA的角平分线. 如图,在△ABC中,AD⊥BC于点D,∠B=60°,∠C=45°,AC=2,则BD的长为
如图,在△ABC中,AD⊥BC于点D,∠B=60°,∠C=45°,AC=2,则BD的长为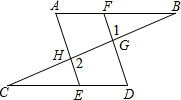 填写下列解题过程中的推理根据:
填写下列解题过程中的推理根据: