题目内容
在代数式x2-4x+7中:
(1)当x=-1时,此代数式的值为
(2)当x= 时,此代数式最小,最小值为 .
(1)当x=-1时,此代数式的值为
(2)当x=
考点:配方法的应用,非负数的性质:偶次方,代数式求值
专题:
分析:(1)把x=-1代入已知代数式并求值即可;
(2)利用配方法来求最值.
(2)利用配方法来求最值.
解答:解:(1)把x=-1代入x2-4x+7,得
x2-4x+7=(-1)2-4×(-1)+7=1+4+7=12.
故答案是:12;
(2)令y=x2-4x+7.
则y=(x-2)2-4+7=(x-2)2+3.
∵(x-2)2≥0,
∴当x-2=0即x=2时,y最小值=3.
故答案是:2;3.
x2-4x+7=(-1)2-4×(-1)+7=1+4+7=12.
故答案是:12;
(2)令y=x2-4x+7.
则y=(x-2)2-4+7=(x-2)2+3.
∵(x-2)2≥0,
∴当x-2=0即x=2时,y最小值=3.
故答案是:2;3.
点评:本题考查了配方法的应用、非负数的性质以及代数式求值.解题时要注意配方法的步骤.注意在变形的过程中不要改变式子的值.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
某种蛋白质分子的直径为251000埃,已知1埃=10-10米,则用科学记数法表示该蛋白质分子的直径是( )
| A、2.51×105米 |
| B、2.51×104米 |
| C、2.51×10-6米 |
| D、2.51×10-5米 |
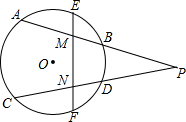 如图,已知圆O的弦AB、CD的延长线相交于点P,连接弧AB、弧CD的中点E、F分别交AB、CD于点M、N,求证:△PNM是等腰三角形.
如图,已知圆O的弦AB、CD的延长线相交于点P,连接弧AB、弧CD的中点E、F分别交AB、CD于点M、N,求证:△PNM是等腰三角形.